Next: Def.
Up: Statistical preliminaries
Previous: Random variables and random
Contents
Let  be a random variable.
We can determine a function
be a random variable.
We can determine a function
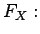

 (called the
cumulative distribution - CDF -
or simply distribution function
of
(called the
cumulative distribution - CDF -
or simply distribution function
of  )
given by
)
given by
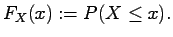 |
(1.4) |
Clearly if  then
then
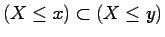 and hence
and hence
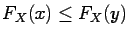 , that is,
, that is, 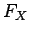 is monotonically increasing.
Furthermore, when
is monotonically increasing.
Furthermore, when
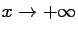 the event
the event 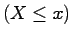 tends to
tends to
 and when
and when
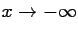 the event
the event 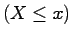 tends to
tends to
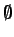 .
Hence it is reasonable that
.
Hence it is reasonable that
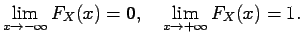 |
(1.5) |
The plots of cumulative distribution functions have the general form shown
in figures 1.1 or 1.2.
Figure 1.1:
A continuous CDF
|
|
Figure 1.2:
A discrete CDF
|
|
How can we determine the cumulative distribution function of a given
random variable  ?
We can sample values of
?
We can sample values of  , repeating
, repeating 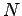 times the corresponding
experiment, obtaining for each
times the corresponding
experiment, obtaining for each
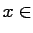
 the table of results:
the table of results:
| Repetition |
Observation |
 ? ? |
| 1 |
 |
yes |
| 2 |
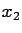 |
no |
| &vellip#vdots; |
&vellip#vdots; |
&vellip#vdots; |
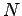 |
 |
yes |
Clearly
if 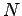 is large, according to the frequency approach.
The function
is large, according to the frequency approach.
The function 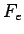 given by
is called
the empirical cumulative distribution function
of
given by
is called
the empirical cumulative distribution function
of  .
If
.
If
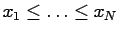 , it has a plot of the form represented in
figure 1.2.
, it has a plot of the form represented in
figure 1.2.
Subsections




Next: Def.
Up: Statistical preliminaries
Previous: Random variables and random
Contents
Mario Putti
2003-10-06
![]() be a random variable.
We can determine a function
be a random variable.
We can determine a function
![]()
![]()
![]()
![]() (called the
cumulative distribution - CDF -
or simply distribution function
of
(called the
cumulative distribution - CDF -
or simply distribution function
of ![]() )
given by
)
given by
![]() ?
We can sample values of
?
We can sample values of ![]() , repeating
, repeating ![]() times the corresponding
experiment, obtaining for each
times the corresponding
experiment, obtaining for each
![]()
![]() the table of results:
the table of results: