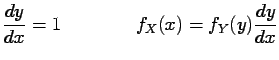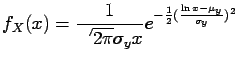Next: Expected Value
Up: Distributions
Previous: Def.
Contents
A random variable has a cumulative distribution 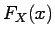 if
if
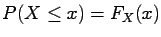 . Examples of cumulative distributions
and their relative density functions are given below.
. Examples of cumulative distributions
and their relative density functions are given below.
- Exponential density function:
The random variable
 has the cumulative distribution (shown
in figure 1.3):
has the cumulative distribution (shown
in figure 1.3):
Figure 1.3:
Exponential distribution.
|
|
- standard Gaussian (Normal) distribution (
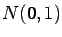 ):
):
and
called the standard Gaussian distribution.
If
 then we have the Gaussian distribution with
mean
then we have the Gaussian distribution with
mean 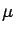 and variance
and variance  (
(
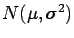 ):
):
and
Figure 1.4:
Gaussian cumulative distribution
|
|
- Lognormal distribution:
let 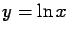 and
and
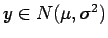 is a lognormal random
variable. Then, since
is a lognormal random
variable. Then, since
Figure 1.5:
Lognormal cumulative distribution
|
|




Next: Expected Value
Up: Distributions
Previous: Def.
Contents
Mario Putti
2003-10-06
![]() if
if
![]() . Examples of cumulative distributions
and their relative density functions are given below.
. Examples of cumulative distributions
and their relative density functions are given below.
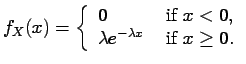
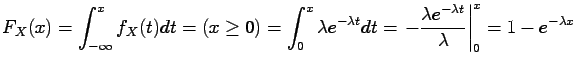
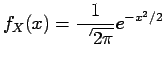

![]() then we have the Gaussian distribution with
mean
then we have the Gaussian distribution with
mean ![]() and variance
and variance ![]() (
(
![]() ):
):
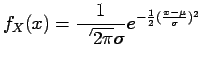
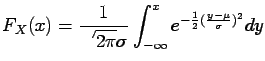
![]() and
and
![]() is a lognormal random
variable. Then, since
is a lognormal random
variable. Then, since