A random variable can take on a large, often infinite, number of values.
We are interested in substituting, in place of the possible values of the
random variable, a representative value that takes into account the
large or small probabilities associated with the RV.
This value is called the Expected Value or Expectation (in italiano
valore atteso o speranza matematica) and its symbol is ![]() .
In the discrete case we can define such a value as an average
of the observations weighted with the respective probabilities, while
in the continuous case we need to substitute sums with integrals:
.
In the discrete case we can define such a value as an average
of the observations weighted with the respective probabilities, while
in the continuous case we need to substitute sums with integrals:
![$\displaystyle E[X] = \sum_{k=1}^\infty x_k p_k
$](img122.gif)
![$\displaystyle E[\phi(X)] = \sum_{k=1}^\infty \phi(x_k) p_k
$](img124.gif)
![$\displaystyle E[X] = \int_{-\infty}^{+\infty} t f_X(t) dt
$](img125.gif)
![$\displaystyle E[\phi(X)] = \int_{-\infty}^{+\infty} \phi(t) f_X(t) dt
$](img126.gif)
Examples:
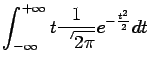 |
|||
 |
|||
| 0 |
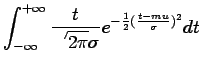 |
|||
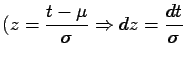 |
|||
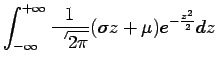 |
|||
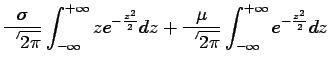 |
|||
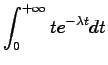 |
|||
| (p.p.) |  |
||
We are also interested in measuring the discrepancies with respect to the expected value. This is accomplished by the ``variance'':
Examples:
 |
|||
| (p.p.) | ![$\displaystyle \frac{1}{\sqrt{2\pi}} \left[\left.
-te^{-\frac{t^2}{2}}\right\vert _{-\infty}^{+\infty}
+ \int_{-\infty}{^{+\infty}e;-\frac{t^2}{2}}dt\right]$](img145.gif) |
||