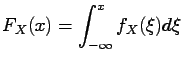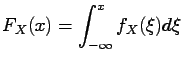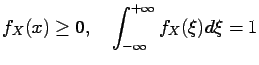Next: Examples of continuous distributions
Up: Distributions
Previous: Distributions
Contents
- A random variable
 is said to be
continuous
if its cumulative distribution function has the form
is said to be
continuous
if its cumulative distribution function has the form
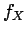 is called the
probability density function
(briefly density) of
is called the
probability density function
(briefly density) of  .
.
Clearly
for any density function 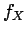 .
.
Mario Putti
2003-10-06