



Next: Distributions
Up: Random Variables
Previous: The concept of Probability
Contents
Random variables and random functions
Let us start with an example related to groundwater hydrology.
- We wish to study the steady state response
of a confined heterogeneous aquifer, under conditions of water
withdrawal.
We measure the hydraulic conductivity at various points in the
aquifer for confidence in the results.
Hence it is convenient to consider modeling the aquifer as a
medium with random characteristics.
To this aim, we perform a pumping test: withdraw water from
a well at specified rates and observe water drawdown at
different wells. By means of pumping test theory, calculate
transmissivities at the different well locations (points in space).
(Note that the number of observation wells is generally small due
to the high drilling costs).
The possible outcomes in our experiment
(i.e. the corresponding profiles of the transmissivities)
are functions which assume a value at each point in the
space which we are working in.
Let
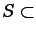

 be the mathematical representation
of this space (the domain of the aquifer).
Then the elements of
be the mathematical representation
of this space (the domain of the aquifer).
Then the elements of  are the functions
are the functions

 where
where

= transmissivity at point

(

).
and we assume that these functions are continuous (
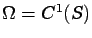 ).
A more classical notation for the random transmissivity at point
).
A more classical notation for the random transmissivity at point  when
the profile is
when
the profile is 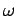 would be:
would be:
 is made up of continuous functions. Let
is made up of continuous functions. Let
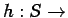
 be the piezometric head (
be the piezometric head (
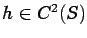 ). The aquifer is confined
and the steady state mass balance equation together with
Neumann (no flow) boundary conditions is:
). The aquifer is confined
and the steady state mass balance equation together with
Neumann (no flow) boundary conditions is:
where 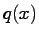 represents the rate of water withdrawal or injection
per unit time and unit volume.
represents the rate of water withdrawal or injection
per unit time and unit volume.
The solution to this boundary value problem is a function
For each point 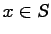 we determine a function
we determine a function
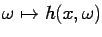 which represents
the piezometric level at the point
which represents
the piezometric level at the point  if the transmissivity rofile in the medium is
if the transmissivity rofile in the medium is
 .
.
The piezometric head is a random function of the random variable 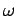 .
Note that a random variable (RV) is also a function from the sample set to
the real axis (
.
Note that a random variable (RV) is also a function from the sample set to
the real axis (

 ), while the random
function
), while the random
function
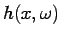 is a function
is a function
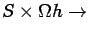
 .
In other words,
.
In other words,
 and
and
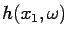 are two
random variables if
are two
random variables if
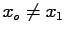 ;
;
 is a realization
of
is a realization
of
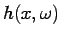 , i.e. the profile (function of
, i.e. the profile (function of  ) of
) of  when
(among all possible observations) only
when
(among all possible observations) only
 is assumed.
is assumed.
In general we are interested in real functions  defined in the
space of outcomes,
and in associating a probability with all the events of the type
defined in the
space of outcomes,
and in associating a probability with all the events of the type
- The value of
 is larger than
is larger than
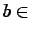
 .
.
- The value of
 is not larger than
is not larger than
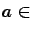
 .
.
- The value of
 falls in the interval
falls in the interval ![$ [a, b]$](img69.gif) , etc.
, etc.
These events will be denoted by means of the symbols
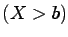 ,
, 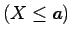 ,
,
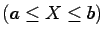 , etc.
, etc.




Next: Distributions
Up: Random Variables
Previous: The concept of Probability
Contents
Mario Putti
2003-10-06
![]()
![]()
![]() be the mathematical representation
of this space (the domain of the aquifer).
Then the elements of
be the mathematical representation
of this space (the domain of the aquifer).
Then the elements of ![]() are the functions
are the functions
![]()
![]() where
where
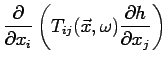
![]() we determine a function
we determine a function
![]() which represents
the piezometric level at the point
which represents
the piezometric level at the point ![]() if the transmissivity rofile in the medium is
if the transmissivity rofile in the medium is
![]() .
.
![]() .
Note that a random variable (RV) is also a function from the sample set to
the real axis (
.
Note that a random variable (RV) is also a function from the sample set to
the real axis (
![]()
![]() ), while the random
function
), while the random
function
![]() is a function
is a function
![]()
![]() .
In other words,
.
In other words,
![]() and
and
![]() are two
random variables if
are two
random variables if
![]() ;
;
![]() is a realization
of
is a realization
of
![]() , i.e. the profile (function of
, i.e. the profile (function of ![]() ) of
) of ![]() when
(among all possible observations) only
when
(among all possible observations) only
![]() is assumed.
is assumed.
![]() defined in the
space of outcomes,
and in associating a probability with all the events of the type
defined in the
space of outcomes,
and in associating a probability with all the events of the type