



Next: Imposizione delle condizioni al
Up: Il codice di calcolo
Previous: Calcolo e assemblaggio dei
Indice
Il contributo locale (11) al termine noto
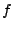 nell'equazione
nell'equazione 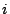 -esima del sistema (9)
per un nodo
-esima del sistema (9)
per un nodo 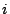 interno al dominio
interno al dominio 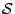 o appartenente a
o appartenente a 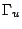 ha espressione:
ha espressione:
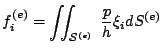 |
(16) |
Nel caso in esame, si è assunto
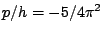 sen
sen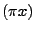 cos
cos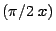 . L'integrale (16) non è facilmente risolubile in
modo esatto e ci limitiamo a ricavarne un'approssimazione per via numerica.
Se la discretizzazione del dominio è sufficientemente fitta, la funzione
. L'integrale (16) non è facilmente risolubile in
modo esatto e ci limitiamo a ricavarne un'approssimazione per via numerica.
Se la discretizzazione del dominio è sufficientemente fitta, la funzione
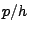 non varia molto all'interno di
non varia molto all'interno di
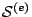 e può quindi essere
trattata come una costante. Approssimiamo
e può quindi essere
trattata come una costante. Approssimiamo 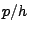 con il valore che essa assume
nel punto
con il valore che essa assume
nel punto
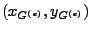 baricentro dell'elemento
baricentro dell'elemento 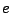 ottenendo:
ottenendo:
che risulta uguale per tutti i nodo appartenenti al medesimo triangolo. Si
dimostra che assemblare i contributi definiti dalla (17) è
equivalente a calcolare la componente 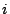 -esima del termine noto globale come:
-esima del termine noto globale come:
dove la sommatoria è estesa a tutti i triangoli che hanno un vertice nel
nodo 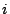 . In sostanza, si può dire che il termine noto è pari al prodotto tra
il termine noto della (1) e l'area di afferenza del nodo
. In sostanza, si può dire che il termine noto è pari al prodotto tra
il termine noto della (1) e l'area di afferenza del nodo 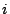 , cioè
1/3 dell'area del patch di triangoli che condividono il nodo
, cioè
1/3 dell'area del patch di triangoli che condividono il nodo 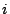 . Può essere
quindi conveniente predisporre un vettore contenente l'area di afferenza
relativa a ciascun nodo della griglia di calcolo.
. Può essere
quindi conveniente predisporre un vettore contenente l'area di afferenza
relativa a ciascun nodo della griglia di calcolo.
Per i nodi situati lungo il boundary  il termine noto locale ha
espressione:
il termine noto locale ha
espressione:
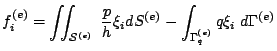 |
(19) |
Alla quantità calcolata mediante la procedura sopra illustrata per i nodi
interni ad 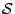 o situati su
o situati su 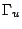 va sottratto un integrale di
bordo esteso a tutti gli elementi contenenti il nodo
va sottratto un integrale di
bordo esteso a tutti gli elementi contenenti il nodo 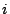 e con un lato posto
su
e con un lato posto
su  . La funzione base
. La funzione base 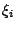 lungo il lato dell'elemento
lungo il lato dell'elemento 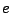 per il
quale
per il
quale 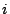 è uno degli estremi si riduce ad una retta che assume valore 1 su
è uno degli estremi si riduce ad una retta che assume valore 1 su
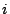 e 0 in corrispondeza all'altro estremo (Figura 4). Utilizzando
ancora la ``midpoint rule'' e ricordando l'espressione di
e 0 in corrispondeza all'altro estremo (Figura 4). Utilizzando
ancora la ``midpoint rule'' e ricordando l'espressione di
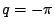 cos
cos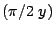 , il secondo integrale della (19) risulta:
, il secondo integrale della (19) risulta:
dove 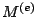 è il punto medio del lato di
è il punto medio del lato di 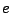 posto su
posto su  ed
ed 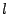 è la sua lunghezza. Come osservato in precedenza, l'assemblaggio dei
contributi (20) al termine noto è equivalente a modificare la
sua componente
è la sua lunghezza. Come osservato in precedenza, l'assemblaggio dei
contributi (20) al termine noto è equivalente a modificare la
sua componente 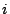 -esima (18) aggiungendo il contributo:
-esima (18) aggiungendo il contributo:
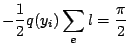 cos cos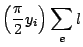 |
(21) |
dove la sommatoria è estesa a tutti i triangoli che hanno un vertice nel nodo
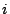 ed un lato su
ed un lato su  . In altri termini, la condizione di Neumann
(3) si impone modificando il termine noto dei nodi situati su
. In altri termini, la condizione di Neumann
(3) si impone modificando il termine noto dei nodi situati su
 ed aggiungendovi l'opposto di
ed aggiungendovi l'opposto di 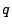 calcolato in
calcolato in 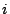 moltiplicato
per la lunghezza del segmento afferente al nodo
moltiplicato
per la lunghezza del segmento afferente al nodo 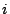 lungo
lungo  , cioè
1/2 della lunghezza totale dei segmenti di bordo che condividono il nodo
, cioè
1/2 della lunghezza totale dei segmenti di bordo che condividono il nodo 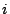 .
Anche in questo caso può essere conveniente predisporre un vettore contenente
la lunghezza del bordo afferente a ciascun nodo su cui viene assegnata una
condizione di Neumann.
.
Anche in questo caso può essere conveniente predisporre un vettore contenente
la lunghezza del bordo afferente a ciascun nodo su cui viene assegnata una
condizione di Neumann.




Next: Imposizione delle condizioni al
Up: Il codice di calcolo
Previous: Calcolo e assemblaggio dei
Indice
Massimiliano Ferronato
2006-11-13
![]() nell'equazione
nell'equazione ![]() -esima del sistema (9)
per un nodo
-esima del sistema (9)
per un nodo ![]() interno al dominio
interno al dominio ![]() o appartenente a
o appartenente a ![]() ha espressione:
ha espressione:
![]() il termine noto locale ha
espressione:
il termine noto locale ha
espressione: