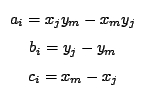Next: Calcolo del termine noto
Up: Il codice di calcolo
Previous: Calcolo della matrice dei
Indice
Figura 3:
Generico elemento triangolare 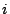 ,
, 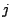 ,
, 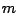 .
.
|
|
Suddividiamo il dominio 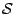 in elementi triangolari
in elementi triangolari 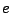 ed indichiamo con
ed indichiamo con
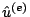 la soluzione approssimata sull'elemento
la soluzione approssimata sull'elemento 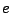 :
:
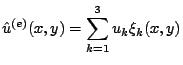 |
(12) |
Nel generico elemento triangolare di Figura 3
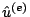 varia
linearmente in funzione delle variabili nodali
varia
linearmente in funzione delle variabili nodali 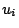 ,
, 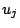 ,
, 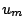 , che
rappresentano la soluzione
, che
rappresentano la soluzione 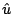 sui nodi
sui nodi 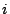 ,
, 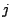 ,
, 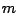 . Le funzioni di
forma
. Le funzioni di
forma 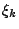 , infatti, sono calcolate utilizzando un'interpolazione lineare e
sono convenientemente scelte in modo tale da:
, infatti, sono calcolate utilizzando un'interpolazione lineare e
sono convenientemente scelte in modo tale da:
- assumere valori non nulli solamente all'interno dell'elemento (supporto
locale);
- valere 1 sul nodo cui sono associate e 0 sugli altri.
Esse assumono pertanto l'espressione:
dove 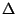 è l'area dell'elemento:
è l'area dell'elemento:
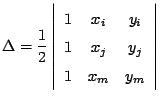
,

i coefficienti 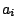 ,
, 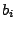 e
e 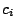 sono dati da:
e gli altri si ottengono con una permutazione degli indici in senso antiorario:
L'andamento delle funzioni basi
sono dati da:
e gli altri si ottengono con una permutazione degli indici in senso antiorario:
L'andamento delle funzioni basi 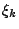 è mostrato in Figura 4.
è mostrato in Figura 4.
Figura 4:
Funzioni base lineari definite sul generico triangolo di vertici
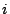 ,
, 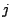 ,
, 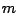 .
.
|
|
Il termine generico della matrice locale del sistema FEM (detta matrice
di rigidezza locale) dalla (10) vale:
![$\displaystyle h_{ij}^{(e)} = \int \!\!\! \int_{{\cal S}^{(e)}} \; \left[ \frac{...
...rtial y} \right] dS^{(e)} = \frac{1}{4 \Delta} \left( b_i b_j + c_i c_j \right)$](img81.gif) |
(14) |
e quindi la matrice di rigidezza locale 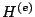 per un elemento triangolare
a 3 nodi si può esprimere come:
per un elemento triangolare
a 3 nodi si può esprimere come:
![$\displaystyle H^{(e)} = \frac{1}{4 \Delta} \left\{ \left[ \begin{array}{ccc} b_...
...& c_j c_j & c_j c_m c_m c_i & c_m c_j & c_m c_m \end{array} \right] \right\}$](img83.gif) |
(15) |
I contributi (15) vanno assemblati nella matrice di rigidezza globale
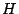 attraverso la matrice dei puntatori TRIJA, costruendo in tal modo
il vettore reale SYSMAT dei termini non nulli della matrice di rigidezza.
attraverso la matrice dei puntatori TRIJA, costruendo in tal modo
il vettore reale SYSMAT dei termini non nulli della matrice di rigidezza.




Next: Calcolo del termine noto
Up: Il codice di calcolo
Previous: Calcolo della matrice dei
Indice
Massimiliano Ferronato
2006-11-13
![\includegraphics[width=8cm]{elemento.eps}](img59.gif)
![]() in elementi triangolari
in elementi triangolari ![]() ed indichiamo con
ed indichiamo con
![]() la soluzione approssimata sull'elemento
la soluzione approssimata sull'elemento ![]() :
:
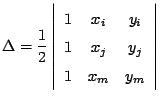 ,
,