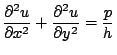Next: Soluzione agli elementi finiti
Up: esercitazione
Previous: Indice
Indice
La deformazione di una membrana elastica sottile, di spessore costante,
perfettamente flessibile, poggiata ed uniformemente tesa al contorno e
caricata ortogonalmente da una pressione costante è governata dall'equazione
differenziale:
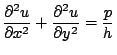 |
(1) |
dove:
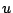 [L]: spostamento verticale dei punti della membrana;
[L]: spostamento verticale dei punti della membrana;
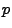 [F/L
[F/L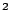 ]: pressione esercitata ortogonalmente alla membrana;
]: pressione esercitata ortogonalmente alla membrana;
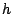 [F/L]: tensione radiale esercitata al bordo.
[F/L]: tensione radiale esercitata al bordo.
Figura 1:
Configurazione geometrica della membrana elastica.
|
|
Nella presente esercitazione si vuole risolvere numericamente il problema
(1) in un dominio quadrangolare 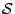 definito come
(Figura 1):
Si ponga
definito come
(Figura 1):
Si ponga 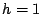 e
e
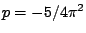 sen
sen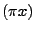 cos
cos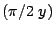 con le seguenti condizioni imposte sulle porzioni
con le seguenti condizioni imposte sulle porzioni 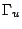 e
e  del
contorno
del
contorno 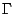 di
di 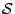 :
:
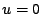 |
lungo |
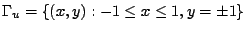 |
(2) |
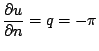 x cos x cos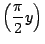 |
lungo |
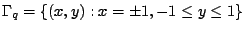 |
(3) |
La soluzione analitica di questo boundary value problem è:
L'equazione (1) con
le condizioni al contorno (2) e (3)
viene risolta
usando il metodo degli elementi finiti (FEM) con elementi triangolari e
funzioni base lineari.
Subsections




Next: Soluzione agli elementi finiti
Up: esercitazione
Previous: Indice
Indice
Massimiliano Ferronato
2006-11-13