



Next: Il codice di calcolo
Up: Formulazione del problema
Previous: Formulazione del problema
Indice
Il funzionale associato all'equazione (1)
e modificato per tener conto delle condizioni al contorno non omogenee
(3)
si scrive:
![$\displaystyle \Omega \left( u \right) = \int \!\!\! \int_{\cal S} \; \left\{ \f...
... \right)^2 \right] + \frac{p}{h} u \right\} dS - \int_{\Gamma_q} q u \; d\Gamma$](img27.gif) |
(5) |
È infatti immediato osservare che l'equazione di Eulero relativa ad 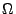 è esattamente la (1). Esso deve essere minimizzato sul dominio
quadrangolare
è esattamente la (1). Esso deve essere minimizzato sul dominio
quadrangolare  soggetto alla condizione al contorno (2).
soggetto alla condizione al contorno (2).
Procediamo seguendo il metodo variazionale di Ritz. Si scriva la soluzione
approssimata 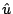 come:
come:
 |
(6) |
dove
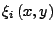 ,
,
 sono opportune funzioni di forma
o funzioni base ed
sono opportune funzioni di forma
o funzioni base ed  corrispondono ai valori puntuali assunti da
corrispondono ai valori puntuali assunti da 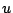 su
su  punti del dominio
punti del dominio  (incognite del problema). Sostituendo
(incognite del problema). Sostituendo
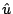 in (5) ed annullando le derivate di
in (5) ed annullando le derivate di
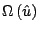 rispetto ai coefficienti
rispetto ai coefficienti  al fine di determinare
la soluzione approssimata che minimizza il funzionale si ottiene:
al fine di determinare
la soluzione approssimata che minimizza il funzionale si ottiene:
![$\displaystyle \frac{\partial \Omega \left( \hat{u} \right)}{\partial u_i} = \in...
...\right] dS = 0 - \int_{\Gamma_q} q \xi_i \; d\Gamma \;\;\;\;\; i = 1, \ldots, n$](img37.gif) |
(7) |
Sostituendo in (7) l'espressione (6) di 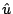 si ha:
si ha:
![$\displaystyle \int \!\!\! \int_{\cal S} \; \left[ \sum_{j=1}^n \left( \frac{\pa...
...- \int_{\Gamma_q} q \xi_i \; d\Gamma \right] dS = 0 \;\;\;\;\; i = 1, \ldots, n$](img38.gif) |
(8) |
Le (8) costituiscono un sistema di  equazioni nelle
equazioni nelle  incognite
incognite
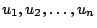 :
:
Il sistema (9) possiede un'infinità di soluzioni e
per renderlo determinato occorre imporre la condizione al contorno (2).
Come funzioni base utilizziamo dei polinomi di interpolazione bidimensionali
continui a tratti e con supporto locale. Pertanto, l'espressione assunta dal
coefficiente 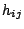 dell'equazione
dell'equazione 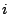 -esima che moltiplica l'incognita
-esima che moltiplica l'incognita  è il risultato dell'assemblaggio dei contributi locali
è il risultato dell'assemblaggio dei contributi locali
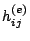 :
:
![$\displaystyle h_{ij} = \sum_e h_{ij}^{(e)} = \sum_e \int \!\!\! \int_{{\cal S}^...
...{\partial \xi_j}{\partial y} \frac{\partial \xi_i}{\partial y} \right] dS^{(e)}$](img47.gif) |
(10) |
mentre il termine noto  della medesima equazione è:
della medesima equazione è:
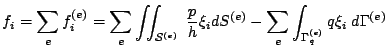 |
(11) |
L'equazione (10) ci permette di osservare che la matrice di rigidezza
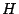 è simmetrica e definita positiva. In più, la scelta di utilizzare
come funzioni base dei polinomi a supporto locale fa sì che
è simmetrica e definita positiva. In più, la scelta di utilizzare
come funzioni base dei polinomi a supporto locale fa sì che
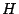 sia anche sparsa. Pertanto il sistema (9) può essere
efficientemente risolto con il metodo del Gradiente Coniugato Modificato (GCM).
sia anche sparsa. Pertanto il sistema (9) può essere
efficientemente risolto con il metodo del Gradiente Coniugato Modificato (GCM).




Next: Il codice di calcolo
Up: Formulazione del problema
Previous: Formulazione del problema
Indice
Massimiliano Ferronato
2006-11-13
![$\displaystyle \Omega \left( u \right) = \int \!\!\! \int_{\cal S} \; \left\{ \f...
... \right)^2 \right] + \frac{p}{h} u \right\} dS - \int_{\Gamma_q} q u \; d\Gamma$](img27.gif)
![]() come:
come:
![]() dell'equazione
dell'equazione ![]() -esima che moltiplica l'incognita
-esima che moltiplica l'incognita ![]() è il risultato dell'assemblaggio dei contributi locali
è il risultato dell'assemblaggio dei contributi locali
![]() :
: