



Next: Applicazione del codice
Up: Il codice di calcolo
Previous: Soluzione del sistema lineare
Indice
Si vuole ora calcolare il primo modo proprio di vibrare della membrana e la
corrispondente lunghezza d'onda. Il problema da risolvere risulta il seguente:
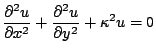 |
(22) |
con le condizioni al contorno definite dalla (2). Nella (22)
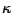 è funzione dello spostamento
è funzione dello spostamento 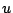 ed è inversamente proporzionale
alla lunghezza d'onda. Dalla teoria del calcolo variazionale si determina che
le lunghezze d'onda ammissibili per la membrana in esame corrispondono ai punti
di stazionarietà, cioè i punti con gradiente nullo, del funzionale:
ed è inversamente proporzionale
alla lunghezza d'onda. Dalla teoria del calcolo variazionale si determina che
le lunghezze d'onda ammissibili per la membrana in esame corrispondono ai punti
di stazionarietà, cioè i punti con gradiente nullo, del funzionale:
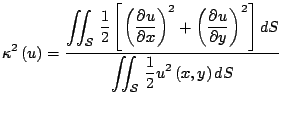 |
(23) |
Fra tutti i punti di stazionarietà posseduti dal funzionale (23), noi
siamo interessati al primo, corrispondente al valore minimo di 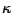 associato al modo di vibrare della membrana con lunghezza d'onda massima.
associato al modo di vibrare della membrana con lunghezza d'onda massima.
Il funzionale (23) si calcola numericamente usando la soluzione
approssimata 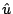 della (6). Si osservi che
della (6). Si osservi che 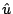 puø
essere riscritta come il seguente prodotto scalare:
puø
essere riscritta come il seguente prodotto scalare:
dove
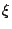 è il vettore delle funzioni forma
è il vettore delle funzioni forma
![$ \left[ \xi_1,
\xi_2, \ldots, \xi_n \right]^T$](img123.gif) . Utilizzando la (24) il numeratore
della (23) risulta:
. Utilizzando la (24) il numeratore
della (23) risulta:
![$\displaystyle \int \!\!\! \int_{\cal S} \; \frac{1}{2} \left[ \left( \frac{\par...
...l y} \frac{\partial \mbox{\boldmath$\xi$}^T}{\partial y} \right] dS \right) \bu$](img124.gif) |
(25) |
Le funzioni forma 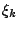 hanno supporto locale e pertanto la matrice definita
dall'espressione integrale che compare nella (25) va calcolata
mediante la consueta procedura di assemblaggio dei contributi derivanti
dai termini locali. L'elemento in riga
hanno supporto locale e pertanto la matrice definita
dall'espressione integrale che compare nella (25) va calcolata
mediante la consueta procedura di assemblaggio dei contributi derivanti
dai termini locali. L'elemento in riga 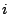 e colonna
e colonna 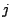 di tale matrice
risulta pertanto:
di tale matrice
risulta pertanto:
![$\displaystyle \sum_e \int \!\!\! \int_{{\cal S}^{(e)}} \; \left[ \frac{\partial...
...\xi_i} {\partial y} \frac{\partial \xi_j}{\partial y} \right] dS^{(e)} = h_{ij}$](img125.gif) |
(26) |
cioè proprio l'elemento in riga 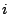 e colonna
e colonna 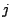 della matrice di rigidezza
della matrice di rigidezza
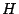 (vedi equazione (10)). Il numeratore del funzionale (23)
approssimato mediante la (6) si può dunque scrivere come:
(vedi equazione (10)). Il numeratore del funzionale (23)
approssimato mediante la (6) si può dunque scrivere come:
![$\displaystyle \int \!\!\! \int_{\cal S} \; \frac{1}{2} \left[ \left( \frac{\par...
...artial \hat{u}}{\partial y} \right)^2 \right] dS = \frac{1}{2} \; \bu^T \bH \bu$](img126.gif) |
(27) |
Procedendo in modo analogo per il denominatore si ottiene:
 |
(28) |
L'espressione integrale definisce una matrice 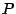 il cui generico elemento
il cui generico elemento
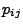 , ottenuto mediante l'assemblaggio dei contributi locali, risulta:
, ottenuto mediante l'assemblaggio dei contributi locali, risulta:
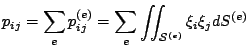 |
(29) |
Pertanto, il denominatore si scrive come:
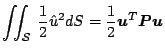 |
(30) |
e la matrice 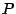 è denominata matrice di capacità della membrana.
Ricordando che:
è denominata matrice di capacità della membrana.
Ricordando che:
 |
(31) |
si ottiene la matrice di capacità locale su un generico elemento triangolare:
![$\displaystyle P^{(e)} = \frac{\Delta}{12} \left[ \begin{array}{ccc} 2 & 1 & 1 1 & 2 & 1 1 & 1 & 2 \end{array} \right]$](img133.gif) |
(32) |
Dalla (29) si può osservare che 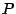 è una matrice simmetrica ed
è facile verificare che è anche definita positiva.
è una matrice simmetrica ed
è facile verificare che è anche definita positiva.
La procedura per assemblare le 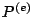 nella
nella 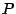 è identica a quella
implementata per assemblare le
è identica a quella
implementata per assemblare le 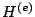 nella
nella 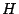 . Si noti anche che la
topologia di
. Si noti anche che la
topologia di 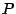 sarà identica a quella di
sarà identica a quella di 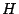 , vale a dire che i vettori
JA ed IA non cambiano.
, vale a dire che i vettori
JA ed IA non cambiano.
L'espressione numerica del funzionale (23), ottenuta discretizzando
numeratore e denominatore secondo la (27) e la (30), è dunque
quella del quoziente di Rayleigh nella forma generalizzata:
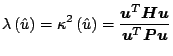 |
(33) |
I vettori che rendono stazionaria la (33) rappresentano i modi di
vibrare della membrana e 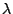 l'inverso del quadrato della corrispondente
lunghezza d'onda. La quantità cercata
l'inverso del quadrato della corrispondente
lunghezza d'onda. La quantità cercata 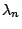 è pertanto l'autovalore
minimo del problema generalizzato:
è pertanto l'autovalore
minimo del problema generalizzato:
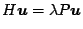 |
(34) |
ed il modo proprio di vibrare il corrispondente autovettore 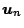 . Tali
quantità possono essere efficientemente determinate minimizzando il quoziente
di Rayleigh generalizzato (33) col metodo del GCM. Anche in questo
caso, affinché il problema sia determinato, è necessario imporre le
condizioni al contorno (2) (membrana fissa al bordo) sia su
. Tali
quantità possono essere efficientemente determinate minimizzando il quoziente
di Rayleigh generalizzato (33) col metodo del GCM. Anche in questo
caso, affinché il problema sia determinato, è necessario imporre le
condizioni al contorno (2) (membrana fissa al bordo) sia su 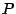 che
su
che
su 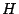 . Si osservi che, tuttavia, l'imposizione delle condizioni al contorno
mediante la procedura indicata in precedenza modifica lo spettro del problema
generalizzato (34) in funzione dei valori
. Si osservi che, tuttavia, l'imposizione delle condizioni al contorno
mediante la procedura indicata in precedenza modifica lo spettro del problema
generalizzato (34) in funzione dei valori 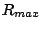 prescelti.
Per evitare di operare sugli ultimi autovalori, e quindi di modificare il
risultato del problema, è consigliabile utilizzare nella matrice
prescelti.
Per evitare di operare sugli ultimi autovalori, e quindi di modificare il
risultato del problema, è consigliabile utilizzare nella matrice 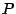 un
valore di
un
valore di 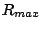 di qualche ordine di grandezza inferiore a quello adottato
in
di qualche ordine di grandezza inferiore a quello adottato
in 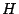 .
.
La convergenza viene raggiunta quando il residuo relativo risulta inferiore
ad una prefissata tolleranza. Si può, ad esempio, adottare la medesima
tolleranza utilizzata per la soluzione del sistema lineare o leggermente
superiore nel caso di una convergenza più difficoltosa.




Next: Applicazione del codice
Up: Il codice di calcolo
Previous: Soluzione del sistema lineare
Indice
Massimiliano Ferronato
2006-11-13
![]() della (6). Si osservi che
della (6). Si osservi che ![]() puø
essere riscritta come il seguente prodotto scalare:
puø
essere riscritta come il seguente prodotto scalare:
![]() nella
nella ![]() è identica a quella
implementata per assemblare le
è identica a quella
implementata per assemblare le ![]() nella
nella ![]() . Si noti anche che la
topologia di
. Si noti anche che la
topologia di ![]() sarà identica a quella di
sarà identica a quella di ![]() , vale a dire che i vettori
JA ed IA non cambiano.
, vale a dire che i vettori
JA ed IA non cambiano.