



Next: About this document ...
Up: esercitazione
Previous: Calcolo del primo modo
Indice
Lo studente implementi un codice di calcolo robusto ed efficiente per la
soluzione numerica del problema descritto nel primo paragrafo della presente
nota mediante la tecnica degli elementi finiti. Si verifichi la correttezza
del codice confrontando la soluzione numerica ottenuta con quella analitica
(4). Quindi si studi la convergenza del metodo quando la dimensione
degli elementi finiti triangolari sia progressivamente ridotta secondo un
fattore costante. Si pensi di raffinare la griglia triangolare secondo lo
schema illustrato in Figura 5. Ogni triangolatura più fine è
ottenuta dalla precedente aggiungendo un nuovo nodo sul punto medio di ciascun
lato. Pertanto ad ogni raffinamento i triangoli quadruplicano. La cosa
interessante è che i nodi delle griglie più grossolane sono un sottoinsieme
di quelle più fini ed il rapporto fra le lunghezze dei lati si dimezza ad ogni
raffinamento.
Figura 5:
Schema di raffinamento della griglia ad elementi finiti.
|
|
Lo studio della convergenza degli elementi finiti alla soluzione analitica
consiste nel raffinare la mesh 3 o 4 volte, risolvere il problema della
deformazione e dell'autovalore/autovettore minimo e verificare i seguenti due
importanti risultati:
- la norma euclidea dell'errore diminuisce come
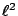 , dove
, dove 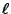 è
una dimensione rappresentativa della triangolazione (in pratica dell'ordine
del lato di un qualsiasi triangolo);
è
una dimensione rappresentativa della triangolazione (in pratica dell'ordine
del lato di un qualsiasi triangolo);
- l'autovalore minimo e l'autovettore ad esso associato convergono ad un
valore limite al progredire del raffinamento della mesh.
La norma euclidea della funzione errore è per definizione:
![$\displaystyle \varepsilon = \left[ \int \!\!\! \int_{\cal S} \; \left( \hat{u} - u \right)^2 dS \right]^{1/2}$](img143.gif) |
(35) |
dove 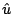 è la soluzione numerica calcolata mediante il codice agli
elementi finiti e
è la soluzione numerica calcolata mediante il codice agli
elementi finiti e 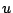 e la soluzione analitica (5). L'integrale
(35) può essere calcolato numericamente mediante la ``midpoint rule'',
vale a dire:
e la soluzione analitica (5). L'integrale
(35) può essere calcolato numericamente mediante la ``midpoint rule'',
vale a dire:
![$\displaystyle \varepsilon = \left\{ \sum_{i=1}^n \left[ \left( \hat{u}_i - u_i \right)^2 \sum_e \frac{\Delta}{3} \right] \right\}^{1/2}$](img144.gif) |
(36) |
in cui la sommatoria sugli elementi 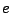 è estesa a tutti i triangoli aventi
in comune il nodo
è estesa a tutti i triangoli aventi
in comune il nodo 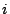 . In pratica, il quadrato della differenza fra la
soluzione numerica e quella analitica su ciascun nodo va pesato con l'area
afferente al nodo già memorizzata per il computo delle componenti del
termine noto.
. In pratica, il quadrato della differenza fra la
soluzione numerica e quella analitica su ciascun nodo va pesato con l'area
afferente al nodo già memorizzata per il computo delle componenti del
termine noto.
Vengono assegnate 4 griglie di calcolo ottenute raffinando regolarmente
la triangolazione iniziale. Per ciascuna griglia vengono inoltre fornite due
versioni, la prima con la numerazione dei nodi originale definita dal
software MeshMaker e la seconda rinumerata in modo da ottimizzare la banda
della matrice di rigidezza del sistema.
Lo studente descriva lo svolgimento dell'esercitazione in una breve
relazione completata dai seguenti allegati minimi:
- tabella di confronto fra la soluzione numerica e quella
analitica per la griglia più grossolana con il calcolo dell'errore puntuale;
- diagrammi di convergenza in scala semilogaritmica del GCM
per la soluzione del sistema: si presenti un diagramma con tutti i profili
di convergenza relativi alle mesh assegnate ottenuti partendo da
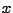
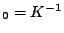
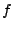 ed utilizzando sia
ed utilizzando sia
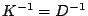 che
che
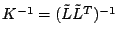 . Si ponga sull'asse
delle ascisse il numero di iterazioni e sull'asse delle ordinate la norma
euclidea del residuo relativo;
. Si ponga sull'asse
delle ascisse il numero di iterazioni e sull'asse delle ordinate la norma
euclidea del residuo relativo;
- diagramma di convergenza in scala semilogaritmica del GCM
per la soluzione del sistema con 1, 2, 5, 10 e 20 iterazioni preliminari
effettuate con lo schema delle Correzioni Residue: per questo test si utilizzi
la mesh più fine usando
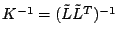 ;
;
- tabella riassuntiva dei risultati in cui siano riportati
ad ogni raffinamento successivo della triangolazione: (a) il valore
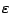 dell'errore, (b) il rapporto fra l'errore corrispondente alla
griglia corrente ed alla griglia meno raffinata immediatamente precedente; (c)
l'autovalore minimo del problema generalizzato.
dell'errore, (b) il rapporto fra l'errore corrispondente alla
griglia corrente ed alla griglia meno raffinata immediatamente precedente; (c)
l'autovalore minimo del problema generalizzato.
- il listato completo del codice di calcolo.
N.B. All'esame non sono ammessi grafici, relazioni e codici
fotocopiati: tutto il materiale deve essere esibito in originale.




Next: About this document ...
Up: esercitazione
Previous: Calcolo del primo modo
Indice
Massimiliano Ferronato
2006-11-13
![\includegraphics[width=11cm]{meshrid.eps}](img140.gif)