



Next: Determinazione dell'autovalore minimo
Up: Rayleigh
Previous: Il metodo delle potenze
Indice
A causa del significato e dell'importanza di 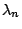 e
e 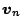 in
molteplici applicazioni di ingegneria civile (corrispondono rispettivamente
alla prima frequenza fondamentale ed al primo modo di vibrare di una struttura
elastica) conviene applicare una tecnica più efficiente del metodo delle
potenze.
in
molteplici applicazioni di ingegneria civile (corrispondono rispettivamente
alla prima frequenza fondamentale ed al primo modo di vibrare di una struttura
elastica) conviene applicare una tecnica più efficiente del metodo delle
potenze.
Si consideri il seguente campo scalare in 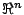 :
:
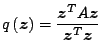 |
(9) |
Si osservi che, se 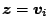 autovettore di
autovettore di 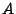 , allora:
, allora:
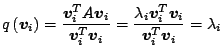 |
(10) |
Inoltre 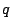 è stazionaria per ogni autovettore di
è stazionaria per ogni autovettore di 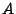 , cioè il gradiente
del campo scalare
, cioè il gradiente
del campo scalare 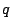 in
in 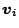 è nullo. Infatti:
è nullo. Infatti:
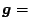 grad grad![$\displaystyle \left[ q \left( \bz \right) \right] = \frac{2}{\bz^T \bz} \left[ A \bz - q \left( \bz \right) \bz \right]$](img41.gif) |
(11) |
e ricordando la (10), si nota immediatamente che 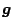 calcolato in
calcolato in
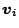 è il vettore nullo per la definizione (1) di autovalori ed
autovettori. Ne consegue, quindi, che i
è il vettore nullo per la definizione (1) di autovalori ed
autovettori. Ne consegue, quindi, che i 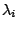 sono massimi o minimi
relativi per
sono massimi o minimi
relativi per 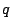 e pertanto dovrà valere:
e pertanto dovrà valere:
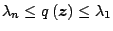 |
(12) |
cioè gli estremi di 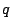 coincidono con gli autovalori estremi di
coincidono con gli autovalori estremi di 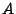 e si
determinano in corrispondenza degli autovettori ad essi collegati. La funzione
e si
determinano in corrispondenza degli autovettori ad essi collegati. La funzione
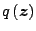 definita in (9), dotata di queste importanti
caratteristiche, è chiamata quoziente di Rayleigh.
definita in (9), dotata di queste importanti
caratteristiche, è chiamata quoziente di Rayleigh.
Subsections




Next: Determinazione dell'autovalore minimo
Up: Rayleigh
Previous: Il metodo delle potenze
Indice
Massimiliano Ferronato
2005-10-19
![]() e
e ![]() in
molteplici applicazioni di ingegneria civile (corrispondono rispettivamente
alla prima frequenza fondamentale ed al primo modo di vibrare di una struttura
elastica) conviene applicare una tecnica più efficiente del metodo delle
potenze.
in
molteplici applicazioni di ingegneria civile (corrispondono rispettivamente
alla prima frequenza fondamentale ed al primo modo di vibrare di una struttura
elastica) conviene applicare una tecnica più efficiente del metodo delle
potenze.
![]() :
: