Ricerca degli autovalori di matrici quadrate

Il problema della ricerca degli autovalori 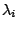$\lambda_i$ e degli autovettori 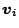$\bv_i$ ad essi associati in una matrice quadrata 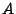$A$ di ordine $n$:

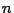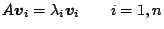$$A \bv_i = \lambda_i \bv_i \;\;\;\;\;\;\; i=1,n$$ (1)

presenta numerose implicazioni a livello ingegneristico in funzione dell'origine della matrice analizzata. Per esempio, se la matrice 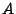$A$ rappresenta la matrice di rigidezza di una struttura elastica, i suoi autovalori ed autovettori corrispondono rispettivamente alle frequenze proprie ed ai modi fondamentali di vibrare, la cui conoscenza costituisce un requisito fondamentale per una corretta progettazione. Un analogo significato viene riscontrato nel caso dell'analisi dinamica di un bacino idrico.

Per tale motivo, oggi esistono numerosi moduli, associati ai programmi in commercio per la soluzione di problemi agli elementi finiti, che consentono la determinazione degli autovalori e degli autovettori della matrice risultante dalla discretizzazione di un modello. Molto spesso l'interesse ingegneristico si concentra sulla conoscenza del solo autovalore massimo o di quello minimo, più raramente risulta necessario determinare l'intero spettro della matrice.