



Next: The variogram
Up: Geostatistics in Hydrology: Kriging
Previous: Evaluation of the estimation
Contents
The hypothesis of second order stationarity of the RF is not always
satisfied, for example 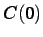 increases with the distance, violating
hypothesis (2.2).
In this case the ``Intrinsic hypothesis'' must be used, in
which we assume that the first order increments
increases with the distance, violating
hypothesis (2.2).
In this case the ``Intrinsic hypothesis'' must be used, in
which we assume that the first order increments
are second order RF:
where the function 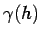 is called the variogram.
If the mean
is called the variogram.
If the mean 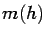 is not zero an obvious change of variable is required.
The variogram is defined as the mean quadratic increment
of
is not zero an obvious change of variable is required.
The variogram is defined as the mean quadratic increment
of  (divided by 2) for any
two points
(divided by 2) for any
two points 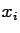 and
and 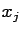 separated by a distance
separated by a distance 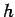 :
:
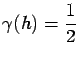 var var![$\displaystyle [Y(x+h) - Y(x)] = \frac{1}{2} E[(Y(x+h) - Y(x))^2]$](img335.gif) |
(2.8) |
and is related to the covariance function by:
The intrinsic hypothesis requires a finite value for the mean of
 but not for its variance. In fact, hypothesis (2.2),
as changed into (2.3), implies (2.8), but not
viceversa.
but not for its variance. In fact, hypothesis (2.2),
as changed into (2.3), implies (2.8), but not
viceversa.
Figure 2.1:
Behavior of the covariance as a function of distance (left) and
the corresponding variogram (right).
|
|
The covariance 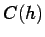 has a decreasing behavior as shown in
Fig. 2.1.
When
has a decreasing behavior as shown in
Fig. 2.1.
When 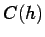 is known then the variogram can be directly
calculated. When
is known then the variogram can be directly
calculated. When 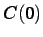 is finite, the variogram
is finite, the variogram 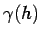 is
bounded asymptotically by this value. The value of
is
bounded asymptotically by this value. The value of 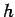 at which
the asymptot can be considered achieved is called the ``range``,
while
at which
the asymptot can be considered achieved is called the ``range``,
while 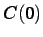 is called the ``sill'' (see Fig. 2.1).
is called the ``sill'' (see Fig. 2.1).
Subsections




Next: The variogram
Up: Geostatistics in Hydrology: Kriging
Previous: Evaluation of the estimation
Contents
Mario Putti
2003-10-06
![]() increases with the distance, violating
hypothesis (2.2).
In this case the ``Intrinsic hypothesis'' must be used, in
which we assume that the first order increments
increases with the distance, violating
hypothesis (2.2).
In this case the ``Intrinsic hypothesis'' must be used, in
which we assume that the first order increments
![$\displaystyle \frac{1}{2} E[(Y(x+h) - Y(x))^2]$](img337.gif)
![$\displaystyle \frac{1}{2} E[Y^2(x+h)] - E[Y(x+h)Y(x)] + \frac{1}{2} E[Y^2(x)]$](img338.gif)
![\includegraphics[width=15cm]{cov_var.eps}](img340.gif)
![]() has a decreasing behavior as shown in
Fig. 2.1.
When
has a decreasing behavior as shown in
Fig. 2.1.
When ![]() is known then the variogram can be directly
calculated. When
is known then the variogram can be directly
calculated. When ![]() is finite, the variogram
is finite, the variogram ![]() is
bounded asymptotically by this value. The value of
is
bounded asymptotically by this value. The value of ![]() at which
the asymptot can be considered achieved is called the ``range``,
while
at which
the asymptot can be considered achieved is called the ``range``,
while ![]() is called the ``sill'' (see Fig. 2.1).
is called the ``sill'' (see Fig. 2.1).