The estimation variance is defined as the variance of the error:
![\begin{multline*}
E[(Y^\ast_0- Y_0)] = E[Y^\ast_0] - E[Y_0]=
\sum_i \lambda_i E[Y_i] - E[Y_0] = 0 \\
(E[Y]=m=0)
\end{multline*}](img310.gif)
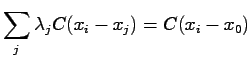
| var |
|||
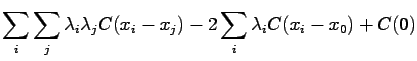 |
|||
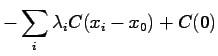 |
|||
var![$\displaystyle [Y] - \sum_i \lambda_i C(x_i-x_0)$](img316.gif) |
It is important to remark the difference between estimation and dispertion
variance. The latter is representative of the variation interval of the
RF ![]() within the interpolation domain, while the estimation variance
represents the residual uncertainty in the estimation of the
realization
within the interpolation domain, while the estimation variance
represents the residual uncertainty in the estimation of the
realization ![]() of
of ![]() when
when ![]() observations are available.
The dispersion variance is a constant, while the estimation variance
varies from point to point and is zero at the observation points.
observations are available.
The dispersion variance is a constant, while the estimation variance
varies from point to point and is zero at the observation points.
Our original variable was ![]() and its estimate is thus:
and its estimate is thus:
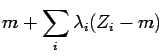 |
|||
| var |
var![$\displaystyle [Z_0] - \sum_i \lambda_i C(x_i-x_0)$](img324.gif) |