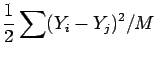The variogram is usually calculated from the experimental observations,
and describes the spatial structure of the RF. It can be
shown (5) that if
![]() are
are ![]() points
belonging to the domain of interpolation and the coefficients
points
belonging to the domain of interpolation and the coefficients
![]() satisfy:
satisfy:
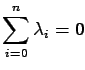
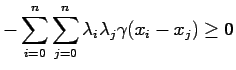
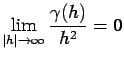
In principle there ![]() could assume different behaviors also with
the direction of vector
could assume different behaviors also with
the direction of vector ![]() (``anisotropy''), but this is in general
not easily verifiable due to the limited number of data points usually
available for hydrologic variables.
If the experimental variogram displays anisotropy, then the intrinsic
hypothesis is not verified and one has to use the so called
``universal'' kriging (2,3).
(``anisotropy''), but this is in general
not easily verifiable due to the limited number of data points usually
available for hydrologic variables.
If the experimental variogram displays anisotropy, then the intrinsic
hypothesis is not verified and one has to use the so called
``universal'' kriging (2,3).
![\includegraphics[width=15cm]{variograms.eps}](img349.gif) |
The most commonly used isotropic variograms are shown in Fig. 2.2 and are of the form:
where
The variogram is estimated from the available observations in the
following manner.
The data points are subdivided into a prefixed number of classes
based on the distances between the measurement locations.
For each pair ![]() and
and ![]() of points and for each class
calculate:
of points and for each class
calculate: