



Next: Case with and known
Up: Geostatistics in Hydrology: Kriging
Previous: Statistical assumptions
Contents
An RF is said to be second order stationary if:
- Constant mean:
![$\displaystyle E[Z(\vec{x},\xi)] = m$](img259.gif) |
(2.1) |
- the autocovariance (another name for the covariance) is a function of
the distance between the reference points
 and
and 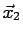 :
:
cov![$\displaystyle [\vec{x}_1,\vec{x}_2] = E[(Z(\vec{x}_1,\xi) - m)(Z(\vec{x}_2,\xi) - m)] = C(\vec{h})$](img262.gif) |
(2.2) |
In practice second order stationarity implies that the first two
statistical moments (expected value and covariance) be translation
invariant. Note that by saying that
![$ E[Z(\vec{x},\xi)] = m$](img263.gif) we imply
that effectively the expected value taken on all the possible
realizations
we imply
that effectively the expected value taken on all the possible
realizations 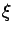 does not vary with space. However, for a given
realization
does not vary with space. However, for a given
realization
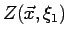 is a function of
is a function of 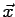 .
.
Because of (2.1), the covariance (2.2) can
be written as:
Obviously if  we have the definition of variance,
also called the ``dispersion'' variance:
we have the definition of variance,
also called the ``dispersion'' variance:
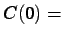
var
![$\displaystyle [Z] = \sigma^2_Z
$](img270.gif)
For simplicity of notation, from now on, we will denote
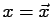 ,
, 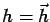 and we will drop the variable
and we will drop the variable 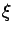 in the
RF.
in the
RF.
Subsections




Next: Case with and known
Up: Geostatistics in Hydrology: Kriging
Previous: Statistical assumptions
Contents
Mario Putti
2003-10-06