



Next: Independence
Up: Statistical preliminaries
Previous: Expected Value
Contents
Consider the example of the confined aquifer in section 1.1.2.
An infinite family 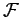 of random variables
of random variables
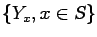 |
(1.6) |
was constructed there, where
is the piezometric head at  corresponding to a transmissivity
profile
corresponding to a transmissivity
profile 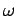 .
.
Suppose a number of points
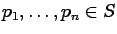 are selected for measurement and let the random variables
are selected for measurement and let the random variables
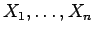 be defined by
be defined by
Then,
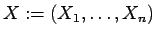 constitutes a
random vector: it is a vector valued random
quantity.
constitutes a
random vector: it is a vector valued random
quantity.
Just as in the scalar case, the probabilities of the
components of a random vector
 are embodied in its joint distribution function
are embodied in its joint distribution function
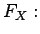

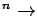
 ,
defined as follows:
,
defined as follows:
For instance if we throw two dice at the same time the outcome of
one does not depend on the outcome of the other. Then we can have:
zsh: command not found: G
if its density is
where 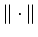 denotes the ordinary Euclidean norm in
denotes the ordinary Euclidean norm in

 .
.
The expectation of a random vector  is defined componentwise:
is defined componentwise:
The covariance matrix of  is defined as:
is defined as:
Cov
![$\displaystyle (X) := E[(X - E[X])(X - E[X])^T]
$](img172.gif)
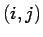 -th element of
Cov
-th element of
Cov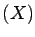 is
and it is referred to as the covariance of
is
and it is referred to as the covariance of  and
and  .
.
A simple computation shows that if
 , then
, then  has
mean
has
mean
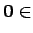

 and its covariance matrix is the identity matrix
and its covariance matrix is the identity matrix
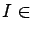

 .
.
Subsections




Next: Independence
Up: Statistical preliminaries
Previous: Expected Value
Contents
Mario Putti
2003-10-06
![]() of random variables
of random variables
![]() are selected for measurement and let the random variables
are selected for measurement and let the random variables
![]() be defined by
be defined by
![]() are embodied in its joint distribution function
are embodied in its joint distribution function
![]()
![]()
![]()
![]() ,
defined as follows:
,
defined as follows:

![]() is defined componentwise:
is defined componentwise:
![]() , then
, then ![]() has
mean
has
mean
![]()
![]()
![]() and its covariance matrix is the identity matrix
and its covariance matrix is the identity matrix
![]()
![]()
![]() .
.