Triangolazioni di Delaunay

La forma degli elementi che discretizzano il dominio di integrazione è di fondamentale importanza per la bontà del risultato ottenuto. Si può infatti dimostrare per via teorica che la convergenza della soluzione approssimata alla soluzione vera di un problema è tanto migliore quanto più la griglia di calcolo è regolare, nel senso che gli angoli interni di elementi adiacenti risultano prossimi fra di loro.

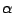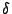La Figura 2 riporta due esempi di elementi triangolari adiacenti. Nel primo caso la mesh risultante è regolare, mentre nel secondo la presenza di angoli ottusi provoca una notevole irregolarità nello schema. È buona norma nella triangolazione di un dominio piano seguire la seguente condizione sugli angoli $\alpha$ e $\delta$ di Figura 2:

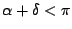$$\alpha + \delta < \pi$$ (2)

In altre parole, si cerca di soddisfare la condizione che la somma di angoli opposti ad un lato in comune fra triangoli adiacenti sia minore di un angolo piatto. Da un punto di vista geometrico, la condizione (2) impone che, considerato il cerchio circoscritto ad ogni elemento triangolare, nessun altro nodo oltre a quelli dell'elemento in esame cada al suo interno (Figura 3). Qualora la condizione (2) sia verificata per tutti gli elementi triangolari con i quali è stato discretizzato il dominio di interesse, si dice che la griglia è una triangolazione di Delaunay. Realizzare una triangolazione di Delaunay è condizione necessaria per assicurare un migliore condizionamento alla matrice del sistema finale e per ottenere una buona convergenza alla soluzione vera. Con mesh irregolari, invece, la soluzione numerica può presentare oscillazioni incontrollate e manifestare segni di instabilità.

Ottenere una triangolazione di Delaunay in un dominio qualsiasi può essere un'operazione estremamente complessa. Per tale motivo, è fondamentale utilizzare uno strumento di calcolo automatico rigoroso ed efficiente. Fra i vari codici in commercio, si è scelto di adottare il software MeshMaker sviluppato e rilasciato dalla società internazionale Argus One.

Figura 2: Esempi di triangolazione regolare ed irregolare.

Figura 3: Interpretazione geometrica della condizione di Delaunay.