



Next: Validation of the interpolation
Up: Geostatistics in Hydrology: Kriging
Previous: Remarks about Kriging
Contents
We now assume that the observations 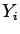 are affected by
measurement errors
are affected by
measurement errors
 , and that:
, and that:
- the errors
 have zero mean:
have zero mean:
- the errors are uncorrelated:
cov
![$\displaystyle [\epsilon_i,\epsilon_j]=0 \qquad\qquad i\ne j
$](img373.gif)
- the errors are not correlated with the RF:
cov
![$\displaystyle [\epsilon_i,Y_i]=0
$](img374.gif)
- the variance
 of the errors is a known quantity and
can vary from point to point.
of the errors is a known quantity and
can vary from point to point.
The new coefficient matrix  of the linear system (2.5)
is changed by adding to the main diagonal the quantity
of the linear system (2.5)
is changed by adding to the main diagonal the quantity
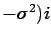 :
and everything proceeds as in the standard case.
:
and everything proceeds as in the standard case.
Mario Putti
2003-10-06
![]() are affected by
measurement errors
are affected by
measurement errors
![]() , and that:
, and that:
![$\displaystyle C + \left[
\begin{array}{ccc}
\sigma^2_1 & \cdot & 0 \\
0 & \cdot & 0 \\
0 & \cdot & \sigma^2_n \\
\end{array}\right]
$](img377.gif)