Case with $m$ and $C(\vec{h})$ known

If $[Z(x)]=m$ and $C(h)$ are known, then we can define a new variable $Y(x)$ with zero mean:

$$Y(x) = Z(x) - m$$

$$E[Y(x)] =$$ 0

Given the observed values:

$$\begin{array}{cccc} x_1 & x_2 & \ldots & x_n \\ Y_1 & Y_2 & \ldots & Y_n \end{array}$$

with $Y_i=Y(x_i)$ being the observation at point $x_i$. we look for a linear estimator $Y^\ast(x_0)$ of $Y(x_0)$ at point $x_0$ using the observed values. The form of the estimator is:

$$Y^\ast (x_0) = \sum_{i=1}^n \lambda_i Y_i$$ (2.4)

Note that the estimator (2.4) is a realization of the RF

$$Y^\ast(x_0,\xi) = \sum_{i=1}^n \lambda_i Y(x_i,\xi)$$

The weights $\lambda_i$ are calculated by imposing that the statistical error

$$\epsilon(x_0) = Y(x_0) - Y^\ast(x_0)$$

has minimum variance:

   var$$[\epsilon(x_0)] = E[(Y(x_0) - Y^\ast(x_0))^2] =$$   minimum

Substituting eq. (2.4) in the expression of the variance we have:

$$E[(Y(x_0) - Y^\ast(x_0))^2] = E[(\sum_{i=1}^n \lambda_i Y_i - Y_0)^2]$$

$$= E[(\sum_{i=1}^n \lambda_i Y_i - Y_0)(\sum_{i=1}^n \lambda_i Y_i - Y_0)]$$

$$= E[(\sum_{i=1}^n \lambda_i Y_i)(\sum_{i=1}^n \lambda_i Y_i)] - 2 E[\sum_{i=1}^n \lambda_i Y_i Y_0] + E[Y_0^2]$$

$$= \sum_{i=1}^n\sum_{j=1}^n \lambda_i\lambda_j E[Y_iY_j] - 2 \sum_{i=1}^n E[Y_iY_0] + E[Y_0^2]$$

but, since $m=0$

$$E[Y_iY_j] = C(x_i-x_j) + m^2 = C(x_i-x_j)$$

and

$$E[Y_0^2] = C(0)=$$   var$$[Y]$$

is the dispersion variance of $Y$. Then:

$$\begin{multline*} E[(Y(x_0) - Y^\ast(x_0))^2] = \sum_{i=1}^n\sum_{j=1}^n \lamb... ...da_j C(x_i-x_j) - 2 \sum_{i=1}^n \lambda_i C(x_i-x_0) \ +C(0) \end{multline*}$$

The minimum is found by setting to zero the first partial derivatives:

$$\begin{multline*} \frac{\partial}{\partial \lambda_i} \left( E[(Y(x_0) - Y^\ast... ...j=1}^n \lambda_j C(x_i-x_j) - 2 C(x_i-x_0) = 0 \\ j=1,\ldots,n \end{multline*}$$

This yields a linear system of equations:

$$C \lambda = b$$ (2.5)

where matrix $C$ is given by:

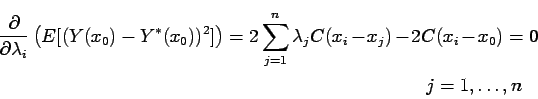
$$C = \left[ \begin{array}{cccc} C(0) & C(x_1-x_2) & \ldots & c(x_1... ...& \cdot \\ \cdot & & \cdot & \\ C(x_n-x_1) & & & C(0) \\ \end{array}\right]$$

and the right hand side vector $b$ is given by:

$$b = \left[ \begin{array}{c} C(x_1-x_0) \\ \cdot \\ \cdot \\ \cdot \\ C(x_n-x_0) \\ \end{array}\right]$$

Matrix $C$ is the spatial covarianve matrix and does not depend upon $x_0$. It can be shown that if all the $x_j$'s are distinct then $C$ is positive definite, and thus the linear system (2.5) can be solved with either direct or iterative methods. Once the solution vector $\lambda$ is obtained, equation (2.4) yields the estimation of our regionalized variable at point $x_0$. Thus the calculated value for $\lambda$ is actually function of the estimation point $x_0$. If we want to change the estimation point $x_0$, for example if we need to obtain a spatial distribution of our regionalized variable, we need to solve the linear system (2.5) for different values of $x_0$. In this case it is convenient to factorize matrix $C$ using Cholseky decomposition and then proceed to the solution for the different right hand side vectors.