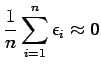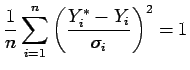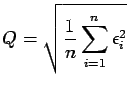Next: Computational aspects
Up: Geostatistics in Hydrology: Kriging
Previous: Kriging with uncertainties
Contents
The chosen model (in practice the variogram) can be validated
by interpolating observed values. If  observations
observations
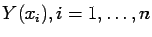 are available, the validation
process proceeds as follows:
are available, the validation
process proceeds as follows:
For each  ,
,
 :
:
- discard point
 ;
;
- estimate the
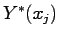 by solving the kriging
system having set
by solving the kriging
system having set  and using the remaining
points
and using the remaining
points
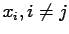 for the interpolation;
for the interpolation;
- evaluate the estimation error
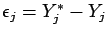 ,
,
The chosen model can be considered theoretically valid if the error
distribution is approximately gaussian with zero mean and unit variance
(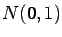 , i.e. satisfies the following:
, i.e. satisfies the following:
- there is no bias:
- the estimation variance
 is coherent with the error
standard deviation:
is coherent with the error
standard deviation:
One can also look at the behavior of the interpolation
error at each point looking at the mean square error of the vector 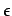 :
The uncertainties connected to the choice of the theoritcal
variogram from the experimental data can be minimized by
anaylizing the validation test. In fact,
among all the possible variograms
:
The uncertainties connected to the choice of the theoritcal
variogram from the experimental data can be minimized by
anaylizing the validation test. In fact,
among all the possible variograms 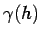 , that close to the origin
display a slope compatible with the obesrvations and gives rise to a
theoretically coherent model, one can choose the variogram
with the smallest value of
, that close to the origin
display a slope compatible with the obesrvations and gives rise to a
theoretically coherent model, one can choose the variogram
with the smallest value of 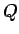 .
.




Next: Computational aspects
Up: Geostatistics in Hydrology: Kriging
Previous: Kriging with uncertainties
Contents
Mario Putti
2003-10-06
![]() observations
observations
![]() are available, the validation
process proceeds as follows:
are available, the validation
process proceeds as follows:
![]() ,
,
![]() :
:
![]() , i.e. satisfies the following:
, i.e. satisfies the following: