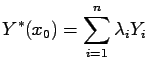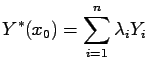Next: Kriging with uncertainties
Up: Geostatistics in Hydrology: Kriging
Previous: Remark 2.
Contents
- Kriging is a BLUE (Best Linear Unbiased Estimator)
interpolator. In other word it is a Linear estimator that
matches the correct expected value of the population (Unbiased)
and that minimizes the variance of the observations (Best).
- Kriging is an exact interpolator if no errors are present.
In fact, if we set
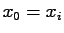 in (2.5) we obtain
immediately
in (2.5) we obtain
immediately
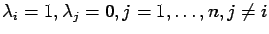 .
.
- If we assume that the the error
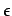 is Gaussian, then
we can associate to the estimate
is Gaussian, then
we can associate to the estimate
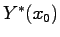 a confidence
interval. For example, the 95% confidence interval is
a confidence
interval. For example, the 95% confidence interval is
 where:
Then the krigin estimator (2.4 becomes:
where:
Then the krigin estimator (2.4 becomes:
- The solution of the linear system does not depend on the observed
value but only on
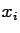 and
and 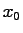 .
.
- A map of the estimated regionalized variable, and possibly its
confidence intervals, can be obtained be defining a grid and solving
the linear system for each point in the grid.
Mario Putti
2003-10-06