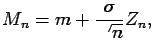Next: Geostatistics in Hydrology: Kriging
Up: Random Vectors
Previous: Random Vectors
Contents
The
conditional probability of  given
given 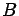 is defined as
is defined as
provided both  and
and 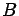 are events and
are events and
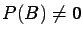 .
.
One can say that  and
and 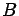 are
independent
if
are
independent
if
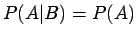 and
and
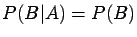 .
Thus
.
Thus  and
and 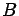 are independent if and only if
are independent if and only if
 |
(1.7) |
Clearly, this last condition makes sense even if either 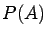 or
or 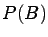 vanishes, hence can be (and usually is) taken as the definition of
independence of
vanishes, hence can be (and usually is) taken as the definition of
independence of  and
and 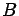 .
.
Two random variables  and
and 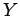 are
independent
if the events
are
independent
if the events 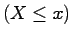 and
and 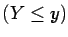 are independent in the sense
of (1.7) for each choice of
are independent in the sense
of (1.7) for each choice of

 , i.e. if
, i.e. if
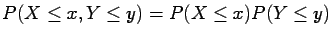 |
(1.8) |
In other words  and
and 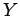 are independent if and only if
are independent if and only if
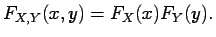 |
(1.9) |
A random vector
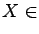

 has
independent components
if all its marginals
has
independent components
if all its marginals
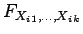 have the multiplicative
property
have the multiplicative
property
for each ordered 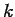 -tuple
-tuple
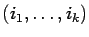 with
with
 with
with 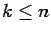 .
N.B. It does not suffice to ask that
.
N.B. It does not suffice to ask that
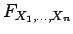 have the multiplicative property for
have the multiplicative property for 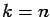 only.
only.
If  and
and 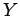 have a joint density
have a joint density  , then both
, then both  and
and 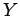 have a
density (
have a
density (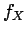 and
and 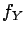 , respectively), namely the marginals
, respectively), namely the marginals
The vectors  and
and 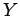 are independent with a joint density
are independent with a joint density 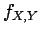 , then
, then
 |
(1.10) |
Conversely, if the joint density factors into the marginal densities,
then (1.9) holds.
Thus (1.10) is a necessary and sufficient condition for
independence.
Let  and
and 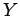 be independent and let
be independent and let 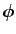 and
and 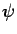 be ``regular''
functions.
Then:
be ``regular''
functions.
Then:
i.e. under independence of  and
and 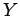 ,
,
![$\displaystyle E[\phi(X) \psi(Y)]= E[\phi(X)] E[\psi(Y)]$](img216.gif) |
(1.11) |
In particular, if 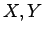 are independent, then
are independent, then
Cov
![$\displaystyle [X, Y] = \left( \begin{array}{cc}
\mbox{Var}[X] & 0 \ 0 & \mbox{Var}[Y] \end{array} \right)
$](img218.gif)
In fact, by (1.11)
Moreover
i.e.
if  and
and 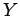 are independent.
are independent.
The above results can be generalized for random vectors.
If an  -dimensional random vector
-dimensional random vector  has independent components,
then
has independent components,
then
and
Let us apply the above results to the following particular situation:
sampling a given random variable, like when a measurement is repeated
a certain number of times.
Suppose  is a given random variable. A sample
of length
is a given random variable. A sample
of length  from
from  is a sequence of independent random variables
is a sequence of independent random variables
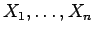 , each of them having the same distribution as
, each of them having the same distribution as  .
The components of the sample are said to be
independent
and identically distributed
(``iid" for short).
The sample mean
.
The components of the sample are said to be
independent
and identically distributed
(``iid" for short).
The sample mean
 |
(1.12) |
is computed in order to estimate the ``value" of  .
.
If
![$\displaystyle E[X] = m,$](img232.gif)
Var
![$\displaystyle [X] = \sigma^2
$](img233.gif)
Then
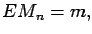 Var Var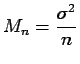 |
(1.13) |
and the advantage of forming the sample average becomes apparent:
While the mean is unaltered, the variance reduces when the number
 of observations increases.
Thus, forming the arithmetic mean of a sample of measurements
results in a higher precision of the estimate.
The situation is as depicted in figure 1.8.
of observations increases.
Thus, forming the arithmetic mean of a sample of measurements
results in a higher precision of the estimate.
The situation is as depicted in figure 1.8.
Figure 1.8:
Density of the sample mean when the number of observations
 increases.
increases.
 width=10cm |
One feels tempted to assert that

as

In fact it is true that
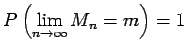 |
(1.14) |
if
 are iid random variables with mean
are iid random variables with mean 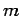 .
This result is known as the
Strong Law of Large Numbers.
.
This result is known as the
Strong Law of Large Numbers.
On the other hand, we know that
![$\displaystyle E[M_n] = m,$](img241.gif)
Var
![$\displaystyle [M_n] = \sigma^2 / n
$](img242.gif)
but we know nothing about the distribution of  . It is true that
. It is true that
![$\displaystyle E[Z_n] = 0,$](img244.gif)
Var
![$\displaystyle [Z_n ]= 1
$](img245.gif)
where
The Central Limit Theorem
states that if
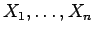 are iid with mean
are iid with mean 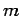 and variance
and variance
 , then
uniformly in
, then
uniformly in
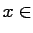
 .
.
Thus, the sample mean is given by
where the normalized errors  are ``asymptotically Gaussian".
are ``asymptotically Gaussian".




Next: Geostatistics in Hydrology: Kriging
Up: Random Vectors
Previous: Random Vectors
Contents
Mario Putti
2003-10-06
![]() given
given ![]() is defined as
is defined as
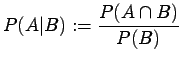
![]() and
and ![]() are
independent
if
are
independent
if
![]() and
and
![]() .
Thus
.
Thus ![]() and
and ![]() are independent if and only if
are independent if and only if
![]() and
and ![]() are
independent
if the events
are
independent
if the events ![]() and
and ![]() are independent in the sense
of (1.7) for each choice of
are independent in the sense
of (1.7) for each choice of
![]()
![]() , i.e. if
, i.e. if
![]()
![]()
![]() has
independent components
if all its marginals
has
independent components
if all its marginals
![]() have the multiplicative
property
have the multiplicative
property
![]() and
and ![]() have a joint density
have a joint density ![]() , then both
, then both ![]() and
and ![]() have a
density (
have a
density (![]() and
and ![]() , respectively), namely the marginals
, respectively), namely the marginals

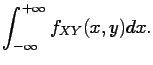
![]() and
and ![]() are independent with a joint density
are independent with a joint density ![]() , then
, then
![]() and
and ![]() be independent and let
be independent and let ![]() and
and ![]() be ``regular''
functions.
Then:
be ``regular''
functions.
Then:
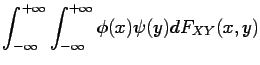

![$\displaystyle [X, Y] = \left( \begin{array}{cc}
\mbox{Var}[X] & 0 \ 0 & \mbox{Var}[Y] \end{array} \right)
$](img218.gif)
![]() -dimensional random vector
-dimensional random vector ![]() has independent components,
then
has independent components,
then
![]() is a given random variable. A sample
of length
is a given random variable. A sample
of length ![]() from
from ![]() is a sequence of independent random variables
is a sequence of independent random variables
![]() , each of them having the same distribution as
, each of them having the same distribution as ![]() .
The components of the sample are said to be
independent
and identically distributed
(``iid" for short).
The sample mean
.
The components of the sample are said to be
independent
and identically distributed
(``iid" for short).
The sample mean