

Next: Esercitazione 1c
Up: Caso transitorio
Previous: Caso transitorio
La soluzione dell'eq. eq23_tran richiede ovviamente l'imposizione
delle condizioni iniziali, oltre che delle condizioni al contorno.
Note le condizioni iniziali, è necessario calcolare la soluzione,
e quindi risolvere il sistema lineare sis_lin_tran,
ad ogni passo temporale.
L'assemblaggio della matrice 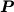 è identico a quello
della matrice di rigidezza
è identico a quello
della matrice di rigidezza 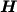 .
Poichè sia
.
Poichè sia 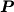 che
che 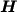 non dipendono dal tempo t
i due assemblaggi vengono effettuati simultaneamente
prima di incominciare il ciclo temporale.
La matrice del sistema ed il termine noto si possono ottenere
ad ogni istante temporale a partire dalle matrici
non dipendono dal tempo t
i due assemblaggi vengono effettuati simultaneamente
prima di incominciare il ciclo temporale.
La matrice del sistema ed il termine noto si possono ottenere
ad ogni istante temporale a partire dalle matrici 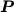 e
e 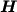 .
.
Come è noto, l'equazione cm_tran ammette soluzione stazionaria,
che si ottiene per 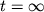 .
E' quindi conveniente incrementare il passo temporale
.
E' quindi conveniente incrementare il passo temporale 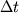 ad ogni istante con progressione geometrica. Cioè
ad ogni istante con progressione geometrica. Cioè
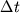 al passo k+1 è ottenuto moltiplicando
al passo k+1 è ottenuto moltiplicando 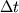 al passo k per un fattore costante, di solito dato in input.
L'aumento di tale fattore comporta una diminuzione del tempo
di simulazione e contemporaneamente l'aumento dell'errore di
troncamento nel tempo.
Empiricamente, il fattore ottimale risulta essere
nell'intorno di 1.2.
al passo k per un fattore costante, di solito dato in input.
L'aumento di tale fattore comporta una diminuzione del tempo
di simulazione e contemporaneamente l'aumento dell'errore di
troncamento nel tempo.
Empiricamente, il fattore ottimale risulta essere
nell'intorno di 1.2.
Per 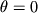 si ottiene come visto il metodo di Eulero esplicito.
In questo caso l'`equazione sis_lin_tran diventa:
si ottiene come visto il metodo di Eulero esplicito.
In questo caso l'`equazione sis_lin_tran diventa:
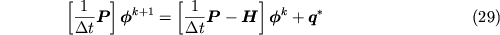
Ad ogni passo temporale si deve risolvere un sistema lineare la cui matrice
coincide praticamente con la matrice  .
Per semplicità, si può utilizzare la tecnica di mass-lumping,
secondo la quale i coefficienti extradiagonali della matrice
.
Per semplicità, si può utilizzare la tecnica di mass-lumping,
secondo la quale i coefficienti extradiagonali della matrice 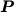 vengono
sommati al corrispondente termine diagonale, ottenendo così una nuova
matrice
vengono
sommati al corrispondente termine diagonale, ottenendo così una nuova
matrice 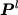 , diagonale, con elementi dati da:
, diagonale, con elementi dati da:
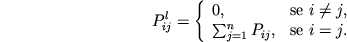
In questo caso, la soluzione del sistema con i gradienti coniugati si ottiene
molto efficientemente con una sola iterazione, ma la condizione di stabilità
impone una restrizione sul passo temporale massimo utilizzabile.
Questo modo di procedere è generalmente meno efficiente del metodo
implicito a causa del grande numero di passi temporali necessari
per ottenere la soluzione al tempo finale.
Le condizioni al contorno di Neumann vengono imposte nello
stesso modo che nel caso stazionario.
Le condizioni al contorno di Dirichlet devono ora essere
imposte sulla matrice del sistema e non solo sulla 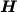 come
nel caso stazionario.
come
nel caso stazionario.


Next: Esercitazione 1c
Up: Caso transitorio
Previous: Caso transitorio
Andrea Pellizzon
Thu Jun 5 11:00:04 MET DST 1997
 è identico a quello
della matrice di rigidezza
è identico a quello
della matrice di rigidezza 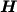 .
Poichè sia
.
Poichè sia 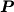 che
che 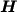 non dipendono dal tempo t
i due assemblaggi vengono effettuati simultaneamente
prima di incominciare il ciclo temporale.
La matrice del sistema ed il termine noto si possono ottenere
ad ogni istante temporale a partire dalle matrici
non dipendono dal tempo t
i due assemblaggi vengono effettuati simultaneamente
prima di incominciare il ciclo temporale.
La matrice del sistema ed il termine noto si possono ottenere
ad ogni istante temporale a partire dalle matrici 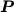 e
e 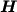 .
.
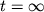 .
E' quindi conveniente incrementare il passo temporale
.
E' quindi conveniente incrementare il passo temporale 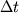 ad ogni istante con progressione geometrica. Cioè
ad ogni istante con progressione geometrica. Cioè
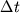 al passo k+1 è ottenuto moltiplicando
al passo k+1 è ottenuto moltiplicando 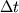 al passo k per un fattore costante, di solito dato in input.
L'aumento di tale fattore comporta una diminuzione del tempo
di simulazione e contemporaneamente l'aumento dell'errore di
troncamento nel tempo.
Empiricamente, il fattore ottimale risulta essere
nell'intorno di 1.2.
al passo k per un fattore costante, di solito dato in input.
L'aumento di tale fattore comporta una diminuzione del tempo
di simulazione e contemporaneamente l'aumento dell'errore di
troncamento nel tempo.
Empiricamente, il fattore ottimale risulta essere
nell'intorno di 1.2.
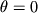 si ottiene come visto il metodo di Eulero esplicito.
In questo caso l'`equazione sis_lin_tran diventa:
si ottiene come visto il metodo di Eulero esplicito.
In questo caso l'`equazione sis_lin_tran diventa:
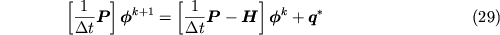
 .
Per semplicità, si può utilizzare la tecnica di mass-lumping,
secondo la quale i coefficienti extradiagonali della matrice
.
Per semplicità, si può utilizzare la tecnica di mass-lumping,
secondo la quale i coefficienti extradiagonali della matrice 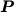 vengono
sommati al corrispondente termine diagonale, ottenendo così una nuova
matrice
vengono
sommati al corrispondente termine diagonale, ottenendo così una nuova
matrice 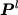 , diagonale, con elementi dati da:
, diagonale, con elementi dati da:
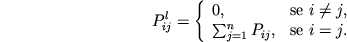
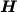 come
nel caso stazionario.
come
nel caso stazionario.