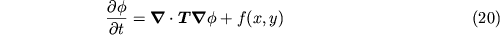
L'equazione conservazione_massa nel caso transitorio si scrive:
con condizioni al contorno e iniziali da specificarsi.
Definiamo una soluzione approssimata di cm_tran del tipo:
dove ora i valori del potenziale ai nodi sono funzioni del tempo t. Le equazioni di Galerkin eq22 diventano quindi:
essendo 
l'area del generico elemento e e 
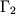il contorno
del dominio ove si impongono condizioni di Neumann.
La eq22_tran si scrive in forma matriciale:
dove il vettore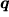 
e la matrice 
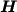sono dati dall'equazione eq25,
mentre la matrice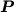 
, detta matrice di capacità, o delle masse, e':
Per l'eq. (10.123) del libro di Gambolati, la matrice di capacità locale a ciascun elemento si può scrivere come:
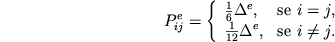
La matr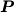ice 
viene calcolata con un procedimento di assemblaggio
identico a quello della matrice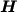 
.
L'equazione eq23_tran è un sistema di equazioni differenziali del primo ordine e si può risolvere usando uno dei metodi alle differenze finite descritti nel paragrafo 8.7, pagina 360 del libro di Gambolati.
Detti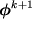 
e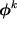 
i vettori dei potenziali nodali
al tempo 
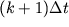e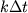 
, rispettivamente, dove
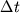è il passo temporale, si pu`o definire il vettore
potenziali al tempo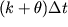 
, ove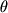 
è un peso
compres tra 0 e 1:
Pensando l'equazione eq23_tran discretizzata al tempo
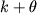possiamo scrivere:
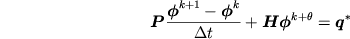
Sostituendo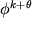 
data dalla pk+theta,
questa equazione si riduce al sistema di equazioni lineari:
E' facile riconoscere lo schema di Eulero in avanti per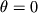 
,
quello di Eulero all'indietro per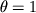 
e quello di Crank Nicolson
per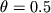 
.
Per la stabilità del primo di tali schemi (cioè lo schema esplicito),
si ricorda che il passo temporale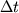 
deve soddisfare la
relazione (eq. (8.63) pag. 363 del Gambolati):
dove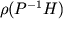 
è il raggio spettrale di 
.
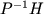Questa relazione pone una restrizione al passo temporale.
Nessuna limitazione è invece neecessaria adottando uno schema
con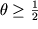 
.
In un problema monodimensionale la stabilita equivale alla relazione
di stabilità dello schema di discretizzazione alle differenze finite
esplicito nel tempo e del secondo ordine nello spazio, come descritto
nel paragrafo 9.10 del Gambolati.
Poichè in problemi monodimensionali la matrice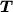 
è uno scalare,
che chiamiamo T, la relazione di stabilità diventa in questo caso:
