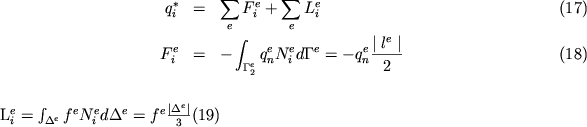
Il vettore dei termini noti dato da (vedi equazione 12):
ove si indicato con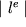 
la lunghezza del segmento
.
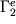Tali termini si riferiscono alle condizioni al contorno di Neumann
(equazione neuman) e alla funzione forzante
(equazione forcing).
Si noti che per l'imposizione della condizione al contorno di flusso
nullo il termine neuman si azzera.
Tale condizione dunque automaticamente assegnata in tutti i nodi
del contorno, se non diversamente specificato.
L'implementazione della funzione forzante avviene generalmente specificando
in input i nodi ove essa definita ed i valori che essa prende.
Ciø richiede la conoscenza dell'area afferente a ciascun nodo.
E' conveniente dunque predisporre gi inizialmente un vettore
contenente per ogni nodo l'area afferente.
L'imposizione delle condizioni di Dirichlet avviene invece preassegnando il valore del potenziale nella fase di soluzione del sistema globale. Per ottenere ciø sarebbe necessario imporre un valore unitario al termine diagonale corrispondente al nodo di Dirichlet, e azzerare tutti gli elementi extradiagonali della riga e colonna corrispondenti, imponendo il valore della condizione di Dirichlet nell'elemento del termine noto corrispondente al nodo.
Alternativamente si puø sostituire l'elemento diagonale della
matrice di rigidezza con un valore molto grande RMAX, e
imporre il valore del termine noto corrispondente
uguale al valore di Dirichlet moltiplicato per RMAX.
In questo modo la condizione al contorno sarebbe soddisfatta
esattamnte se RMAX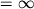
.
Se RMAX è un numero molto grande la condizione è praticamente
soddisfatta.
