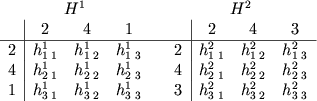

Next: Calcolo del vettore
Up: Il codice di
Previous: Esempio
Si possono ora calcolare gli elementi della matrice di rigidezza H.
La matrice globale viene calcolata tramite un processo di assemblaggio
dei contributi locali di ciascun elemento finito.
Si definisce dunque una matrice di rigidezza locale 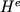 di
dimensione
di
dimensione 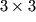 i cui elementi sono dati da:
i cui elementi sono dati da:
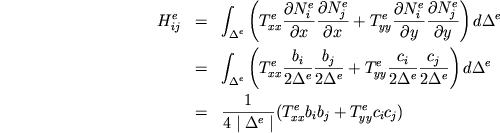
La matrice globale si ottiene tramite l'assemblaggio dei contributi
dei diversi elementi:

Si noti come gli elementi della matrice locale di rigidezza
individuino le righe e le colonne della matrice globale
corrispondenti ai nodi dell'elemento.
Con riferimento sempre al triangolo di vertici i, j e m,
l'elemento 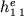 della matrice locale andr sommato
all'elemento diagonale della matrice globale relativo al nodo i, e
dunque all'elemento
della matrice locale andr sommato
all'elemento diagonale della matrice globale relativo al nodo i, e
dunque all'elemento 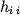 , mentre l'elemento
, mentre l'elemento 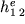 dovr
essere sommato all'elemento della matrice globale relativo ai nodi i
e j:
dovr
essere sommato all'elemento della matrice globale relativo ai nodi i
e j: 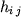 .
Analogamente l'elemento
.
Analogamente l'elemento 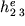 andr a contribuire all'elemento
della matrice globale
andr a contribuire all'elemento
della matrice globale 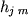 , e cos via.
, e cos via.
Si consideri, per esempio, la mesh di Figura 7,
dove i nodi sono individuati da numeri scritti in carattere normale,
mentre gli elementi sono individuati da numeri scritti in grassetto.
Il nodo centrale 13 circondato dagli elementi 12,13,14 e
19,20,21, che, data la propriet delle funzioni base di avere
supporto locale, saranno gli unici a contribuire all'equazione
relativa al nodo stesso.
La matrice locale 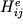 , e= 12,13,14,19,20,21,
riportata in Figura 8.
, e= 12,13,14,19,20,21,
riportata in Figura 8.

Figure 7: Esempio di triangolazione regolare con triangoli
rettangoli.
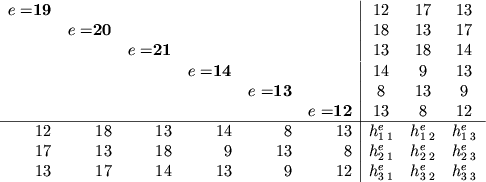
Figure 8: Matrice locale di rigidezza relativa al nodo 13 di
Figura 7. Si noti che gli elementi sono scritti
in carattere grassetto, mentre i nodi sono in carattere normale.
L'assemblaggio viene eseguito calcolando il contributo che ciascun
elemento fornisce all'equazione relativa al nodo 13 (Figura 9)
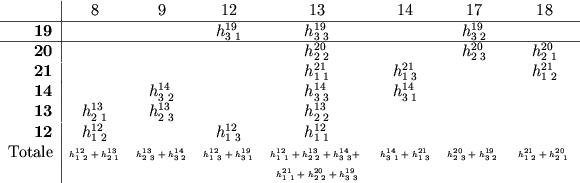
Figure 9: Schema di assemblaggio per l'equazione relativa al nodo 13
L'algoritmo che esegue l'assemblaggio si complica per il fatto che la
matrice di rigidezza globale 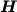 memorizzata in forma compatta.
In pratica tale algoritmo si puø riassumere come segue.
memorizzata in forma compatta.
In pratica tale algoritmo si puø riassumere come segue.
Per ciascun triangolo:
- ordinare in senso crescente i nodi del triangolo e
memorizzare gli indici di posizionamento. Per esempio
memorizzare nel vettore I1 gli indici dell'elemento
ordinati in senso crescente e in I3 le posizioni
iniziali corrispondenti ai nodi di I1.
- Individuare la posizione nella matrice globale di ogni
elemento della matrice locale.
Per ciascun nodo K del triangolo (k=1,3):
- determinare la posizione IND in IAC
dell'elemento diagonale corrispondente al nodo
considerato.
Sommare all'elemento di posizione IND nella
matrice globale COEF l'elemento diagonale della
matrice locale.
- per i rimanenti nodi m (m=k+1,3) scandire in IAC
gli elementi extradiagonali di COEF nella riga
corrispondente al nodo K e determinare la
posizione IND1 che individua il nodo I1(m).
Sommare a COEF in posizione IND1 l'elemento
della matrice locale
corrispondente ai nodi opportuni, e cio
l'elemento di indici I3(k),I3(m).
Per esempio per i triangoli di Figura 5,
la cui tabella data da:

le matrici locali di rigidezza, con indicati gli indici relativi alla posizione
nella matrice globale, sono:
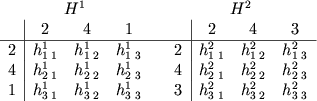
Indicando con COEF la matrice globale memorizzata in modo compatto,
e con HL quella locale, il processo di assemblaggio per tali triangoli
avviene come segue.
elemento 1:
-
- ordinamento
- :
I1 = 1, 2, 4
I3 = 3, 1, 2
-
- k=1
- (primo nodo nella lista)
- m=1
- (nodo diagonale)
IND=IAT(I1(1))=IAT(1)=1 posizione elemento diagonale
COEF(1)=COEF(1)+HL(3,3)
- m=2
- (nodo successivo)
IND1=2 posizione successiva nella riga
IAC(2)=2; individua il nodo 2 nella terna
ordinata: I1(2)=2.
COEF(2)=COEF(2)+HL(3, 1)
- m=3
- (nodo successivo)
IND1=3 posizione successiva nella riga
IAC(3)=4; individua il nodo 4 nella terna
ordinata: I1(3)=4.
COEF(3)=COEF(3)+HL(3, 2)
- k=2
- (secondo nodo nella lista)
- m=2
- (nodo diagonale)
IND=IAT(2)=4 posizione elemento diagonale
COEF(4)=COEF(4)+HL(1,1)
- m=3
- (nodo successivo)
IND1=5 posizione successiva nella riga
IAC(5)=3; individua il nodo 3 nella terna
ordinata: I1(3)=4: non sono uguali, e
quindi non corrispondono.
IND1=6 posizione successiva nella riga
IAC(6)=4; individua il nodo 4 nella terna
ordinata: I1(3)=4.
COEF(6)=COEF(6)+HL(1, 2)
- k=3
- (ultimo nodo nella lista)
- m=3
- (nodo diagonale)
IND=IAT(3)=7 posizione elemento diagonale
COEF(7)=COEF(7)+HL(2,2)
elemento 2:
-
- ordinamento
- :
I1 = 2, 3, 4
I3 = 1, 3, 2
-
- k=1
- (primo nodo nella lista)
- m=1
- (nodo diagonale)
IND=IAT(I1(1))=IAT(2)=4 posizione elemento diagonale
COEF(4)=COEF(4)+HL(1,1)
- m=2
- (nodo successivo)
IND1=5 posizione successiva nella riga
IAC(5)=3; individua il nodo 3 nella terna
ordinata: I1(2)=3.
COEF(5)=COEF(5)+HL(1, 3)
- m=3
- (nodo successivo)
IND1=6 posizione successiva nella riga
IAC(6)=4; individua il nodo 4 nella terna
ordinata: I1(3)=4.
COEF(6)=COEF(6)+HL(1, 2)
- k=2
- (secondo nodo nella lista)
- m=2
- (nodo diagonale)
IND=IAT(3)=7 posizione elemento diagonale
COEF(7)=COEF(7)+HL(3,3)
- m=3
- (nodo successivo)
IND1=8 posizione successiva nella riga
IAC(8)=4; individua il nodo 4 nella terna
ordinata: I1(3)=4.
COEF(8)=COEF(8)+HL(3, 2)
- k=3
- (ultimo nodo nella lista)
- m=3
- (nodo diagonale)
IND=IAT(4)=9 posizione elemento diagonale
COEF(9)=COEF(9)+HL(2,2)


Next: Calcolo del vettore
Up: Il codice di
Previous: Esempio
Andrea Pellizzon
Thu Jun 5 11:00:04 MET DST 1997
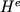 di
dimensione
di
dimensione 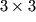 i cui elementi sono dati da:
i cui elementi sono dati da:
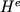 di
dimensione
di
dimensione  i cui elementi sono dati da:
i cui elementi sono dati da:
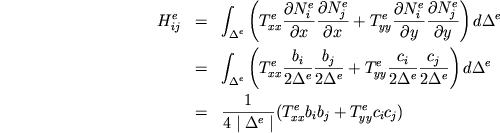

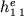 della matrice locale andr sommato
all'elemento diagonale della matrice globale relativo al nodo i, e
dunque all'elemento
della matrice locale andr sommato
all'elemento diagonale della matrice globale relativo al nodo i, e
dunque all'elemento 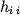 , mentre l'elemento
, mentre l'elemento 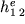 dovr
essere sommato all'elemento della matrice globale relativo ai nodi i
e j:
dovr
essere sommato all'elemento della matrice globale relativo ai nodi i
e j: 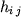 .
Analogamente l'elemento
.
Analogamente l'elemento 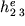 andr a contribuire all'elemento
della matrice globale
andr a contribuire all'elemento
della matrice globale 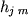 , e cos via.
, e cos via.
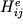 , e= 12,13,14,19,20,21,
riportata in Figura 8.
, e= 12,13,14,19,20,21,
riportata in Figura 8.

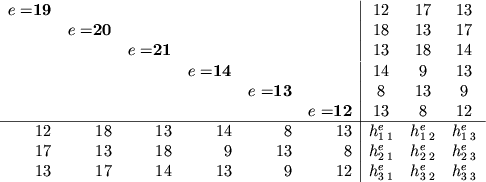
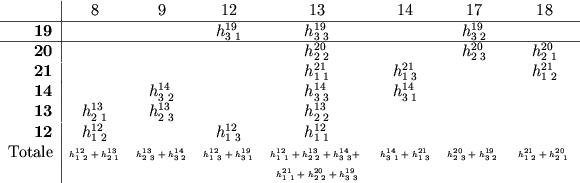
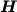 memorizzata in forma compatta.
In pratica tale algoritmo si puø riassumere come segue.
memorizzata in forma compatta.
In pratica tale algoritmo si puø riassumere come segue.