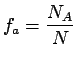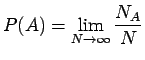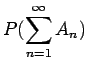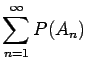Next: Random variables and random
Up: Random Variables
Previous: Random Variables
Contents
A general model for an experiment could be constructed in the
following manner:
- Take a non-empty set
 , in such a way that each
, in such a way that each
 represents a possible outcome
of the experiment.
represents a possible outcome
of the experiment.
- To the ``greatest possible number" of subsets
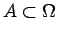 ,
each subset
,
each subset  representing a possible event,
associate a number
representing a possible event,
associate a number
![$ P(A) \in [0,1] $](img9.gif) , called the probability
of such event.
, called the probability
of such event.
An event  has been observed when we perform a ``realization of the
experiment'' and an outcome
has been observed when we perform a ``realization of the
experiment'' and an outcome
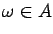 is obtained. The probability
of the event can be defined as follows (``frequentist approach''):
is obtained. The probability
of the event can be defined as follows (``frequentist approach''):
Repeat the experiment 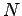 times, with
times, with 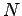 large, and observe the
results. If event
large, and observe the
results. If event  has occurred
has occurred 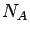 times then
times then
is the relative frequency of event  and is an approximation of
the probability
and is an approximation of
the probability 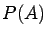 of occurrence of
of occurrence of  . Then
. Then 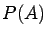 can be
defined as:
In practice the probability is a function relating the elements
of the family of events to the interval
can be
defined as:
In practice the probability is a function relating the elements
of the family of events to the interval ![$ [0,1]$](img1.gif) :
where
:
where
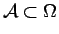 and the following properties
hold:
and the following properties
hold:
for any family
 of events for which
of events for which
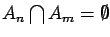 if
if 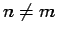 .
.
In mathematical terms the ordered triple
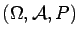 |
(1.1) |
is called a probability space
if
 is a non-empty set (the space of outcomes),
is a non-empty set (the space of outcomes),
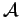 is a family of subsets of
is a family of subsets of  (the family of events),
(the family of events),
-
![$ P : {\cal A} \rightarrow [0,1]$](img28.gif) is a probability.
is a probability.
The structure (1.1) constitutes the basis for a mathematical model
of an experiment, keeping in mind the non-reproducibility which is often
encountered in empirical sciences.
For instance, in a coin toss the outcomes are ``heads'' (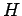 ) or ``tails''
(
) or ``tails''
( ) and we can take
All possible events are elements of
Lastly, if the coin is ``fair", intuitively the probability
) and we can take
All possible events are elements of
Lastly, if the coin is ``fair", intuitively the probability 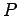 is given by
is given by
All the properties of probability, without exception, are derived
from the mathematical model (1.1).




Next: Random variables and random
Up: Random Variables
Previous: Random Variables
Contents
Mario Putti
2003-10-06
![]() has been observed when we perform a ``realization of the
experiment'' and an outcome
has been observed when we perform a ``realization of the
experiment'' and an outcome
![]() is obtained. The probability
of the event can be defined as follows (``frequentist approach''):
is obtained. The probability
of the event can be defined as follows (``frequentist approach''):
![]() times, with
times, with ![]() large, and observe the
results. If event
large, and observe the
results. If event ![]() has occurred
has occurred ![]() times then
times then