Next: Kriging with moving neighborhoods
Up: Geostatistics in Hydrology: Kriging
Previous: Validation of the interpolation
Contents
In the validation phase  linear systems of dimension
linear systems of dimension 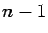 need
to be solved. The system matrices are obtained by dropping
one row and one complumn of the complete kriging matrix. This can be
efficiently accomplished by means of intersections of
need
to be solved. The system matrices are obtained by dropping
one row and one complumn of the complete kriging matrix. This can be
efficiently accomplished by means of intersections of 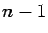 -dimensional
lines with apporpriate coordinate
-dimensional
lines with apporpriate coordinate  -dimensional planes.
-dimensional planes.
Note that the krigin matrix  is symmetric, and thus its eigenvalues
is symmetric, and thus its eigenvalues
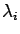 are real. However, since
are real. However, since
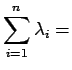
Tr
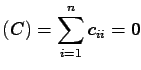
where
Tr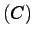 is the trace of matrix
is the trace of matrix  , it follows that some
of the eigenvalues must be negative and thus
, it follows that some
of the eigenvalues must be negative and thus  is not positive
definite.
For this reason, the solution of the linear systems is usually
obtained by means of direct methods, such as Gaussian elimination
or Choleski decomposition. Full Pivoting is often necessary to maintain
stability of the algorithm.
is not positive
definite.
For this reason, the solution of the linear systems is usually
obtained by means of direct methods, such as Gaussian elimination
or Choleski decomposition. Full Pivoting is often necessary to maintain
stability of the algorithm.
Mario Putti
2003-10-06
![]() linear systems of dimension
linear systems of dimension ![]() need
to be solved. The system matrices are obtained by dropping
one row and one complumn of the complete kriging matrix. This can be
efficiently accomplished by means of intersections of
need
to be solved. The system matrices are obtained by dropping
one row and one complumn of the complete kriging matrix. This can be
efficiently accomplished by means of intersections of ![]() -dimensional
lines with apporpriate coordinate
-dimensional
lines with apporpriate coordinate ![]() -dimensional planes.
-dimensional planes.
![]() is symmetric, and thus its eigenvalues
is symmetric, and thus its eigenvalues
![]() are real. However, since
are real. However, since
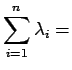 Tr
Tr