Caso simmetrico

Nel caso in cui la matrice $A$ sia simmetrica, come accade ad esempio nella soluzione agli elementi finiti dell'equazione differenziale ellittica di Laplace, il risparmio computazionale derivato dal sistema CRS viene incrementato memorizzando la sola parte triangolare alta, inclusa la diagonale principale, di $A$. In altri termini, vengono memorizzati solo i coefficienti $a_{ij} \neq 0$ con $j \geq i$ e si sfrutta la proprietà di $A$ secondo cui $a_{ij} = a_{ji}$.

La memorizzazione di $A$ viene effettuata sempre mediante i tre vettori SYSMAT, JA e IA definiti nel paragrafo precedente, in cui tuttavia $nt$ rappresenta il numero di coefficienti non nulli della triangolare alta e IA contiene le posizioni in cui si trova in SYSMAT l'elemento diagonale di ciascuna riga di $A$.

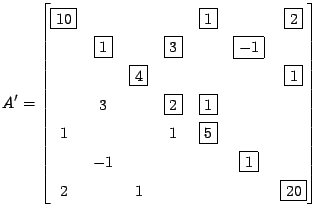
Anche in questo caso facciamo un esempio numerico per rendere più chiaro il concetto. Si consideri la seguente matrice $A$ di dimensione 7$\times$7, sparsa e simmetrica:

$$A = \left[ \begin{array}{rrrrrrr} 10 & 0 & 0 & 0 & 1 & 0 & 2 \\ ... ... -1 & 0 & 0 & 0 & 1 & 0 \\ 2 & 0 & 1 & 0 & 0 & 0 & 20 \\ \end{array} \right]$$

Gli elementi non nulli sono 19, mentre se fosse piena ne avremmo 49. Tuttavia i coefficienti da memorizzare sono solamente quelli relativi alla parte superiore di $A$, di seguito evidenziati:

$$A' = \begin{bmatrix} \boxed{10}& & & & \boxed{1}& & \boxed{2}\\ ... ... & \\ & -1 & & & & \boxed{1}& \\ 2 & & 1 & & & & \boxed{20}\\ \end{bmatrix}$$

Il vettore SYSMAT avrà perciò dimensione $nt=13$ (7 elementi diagonali più 6 extra-diagonali) anziché 19, con un risparmio di memoria superiore al 30%, e sarà dato da:

$$\overbrace{ \begin{array}{rrrrrrrrrrrrrrrrrr} 10 & 1 & 2 & 1 & 3 & -1 & 4 & 1 & 2 & 1 & 5 & 1 & 20 \end{array}}^{nt}$$

Il vettore JA con gli indici di colonna corrispondenti ha la stessa dimensione di SYSMAT e risulta:

$$\overbrace{ \begin{array}{rrrrrrrrrrrrrrrrrr} 1 & 5 & 7 & 2 & 4 & 6 & 3 & 7 & 4 & 5 & 5 & 6 & 7 \end{array}}^{nt}$$

Infine, il vettore IA possiede sempre dimensione $n+1$ ed individua la posizione in SYSMAT degli elementi diagonali:

$$\overbrace{ \begin{array}{rrrrrrrrrrrrrrrrrr} 1 & 4 & 7 & 9 & 11 & 12 & 13 & 14 \end{array}}^{n+1}$$

Ad esempio, IA(3)=7 significa che $a_{33}$ è memorizzato in SYSMAT(7), come confermato anche dal fatto che JA(7)=3.

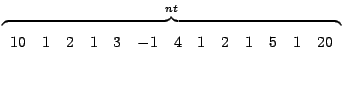
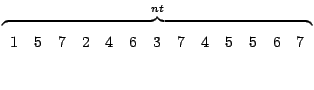
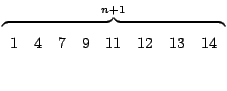
Come nel caso di matrici non simmetriche, si pone IA $(n+1)=nt+1$. Si noti anche che dovrà sempre essere IA(1)=1 e IA$(n)=nt$, nonché JA(1)=1 e JA$(nt)=n$.