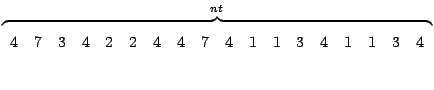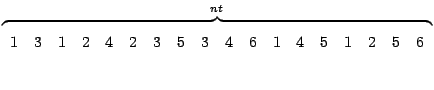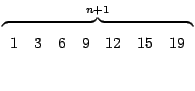Next: Caso simmetrico
Up: Memorizzazione di una matrice
Previous: Memorizzazione di una matrice
Indice
Data una generica matrice 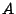 quadrata di ordine
quadrata di ordine 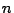 , la tecnica di
memorizzazione CRS prevede la generazione di 3 vettori:
, la tecnica di
memorizzazione CRS prevede la generazione di 3 vettori:
- SYSMAT: vettore di numeri reali contenente gli
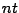 coefficienti non nulli della matrice
coefficienti non nulli della matrice 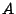 memorizzati in successione per righe;
memorizzati in successione per righe;
- JA: vettore di numeri interi contenente gli
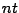 indici di
colonna dei corrispondenti elementi memorizzati in SYSMAT;
indici di
colonna dei corrispondenti elementi memorizzati in SYSMAT;
- IA: vettore di numeri interi con
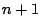 componenti, contenente le
posizioni in cui si trova in SYSMAT il primo elemento di ciascuna riga
di
componenti, contenente le
posizioni in cui si trova in SYSMAT il primo elemento di ciascuna riga
di 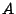 .
.
Il vettore IA è chiamato ``vettore topologico'' e talvolta indicato
anche come TOPOL. L'uso congiunto di IA e JA consente di
individuare qualsiasi elemento non nullo 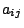 memorizzato in SYSMAT.
Infatti, l'elemento
memorizzato in SYSMAT.
Infatti, l'elemento 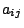 si troverà in una posizione
si troverà in una posizione 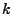 del vettore
SYSMAT compresa nell'intervallo IA
del vettore
SYSMAT compresa nell'intervallo IA
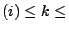 IA
IA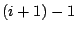 e tale per cui JA
e tale per cui JA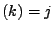 . Queste due condizioni
permettono di individuare univocamente
. Queste due condizioni
permettono di individuare univocamente 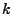 per cui SYSMAT
per cui SYSMAT
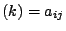 .
Si noti che l'occupazione di memoria si riduce da
.
Si noti che l'occupazione di memoria si riduce da 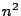 numeri reali
(generalmente in doppia precisione) a
numeri reali
(generalmente in doppia precisione) a 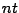 numeri reali (tipicamente
numeri reali (tipicamente
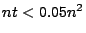 ) e
) e 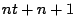 numeri interi.
numeri interi.
Facciamo un esempio numerico per rendere più chiaro il concetto. Si consideri
la seguente matrice 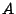 di dimensione 6
di dimensione 6 6, sparsa e non simmetrica:
6, sparsa e non simmetrica:
Gli elementi non nulli sono 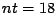 , mentre
, mentre 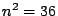 , pertanto il grado di
sparsità di
, pertanto il grado di
sparsità di 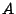 è il 50%. Trascurando i coefficienti nulli, la matrice
è il 50%. Trascurando i coefficienti nulli, la matrice
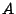 diventa:
Il vettore SYSMAT ha dimensione 18 e risulta:
Il vettore JA ha la stessa dimensione di SYSMAT e per ogni
coefficiente di quest'ultimo individua l'indice di colonna:
Il vettore IA, infine, individua la posizione in SYSMAT del primo
coefficiente di ciascuna riga:
Si noti che che le componenti di IA sono necessariamente ordinate in
senso strettamente crescente e che IA
diventa:
Il vettore SYSMAT ha dimensione 18 e risulta:
Il vettore JA ha la stessa dimensione di SYSMAT e per ogni
coefficiente di quest'ultimo individua l'indice di colonna:
Il vettore IA, infine, individua la posizione in SYSMAT del primo
coefficiente di ciascuna riga:
Si noti che che le componenti di IA sono necessariamente ordinate in
senso strettamente crescente e che IA
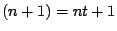 . Ciò si deduce
immediatamente dal fatto che per individuare un elemento
. Ciò si deduce
immediatamente dal fatto che per individuare un elemento 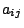 dell'ultima
riga di
dell'ultima
riga di 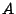 si deve cercare l'indice
si deve cercare l'indice 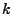 della componente in SYSMAT
nell'intervallo IA
della componente in SYSMAT
nell'intervallo IA
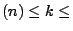 IA
IA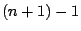 .
.




Next: Caso simmetrico
Up: Memorizzazione di una matrice
Previous: Memorizzazione di una matrice
Indice
Massimiliano Ferronato
2005-09-27
![]() quadrata di ordine
quadrata di ordine ![]() , la tecnica di
memorizzazione CRS prevede la generazione di 3 vettori:
, la tecnica di
memorizzazione CRS prevede la generazione di 3 vettori:
![]() di dimensione 6
di dimensione 6![]() 6, sparsa e non simmetrica:
6, sparsa e non simmetrica:
![$\displaystyle A = \left[ \begin{array}{rrrrrr}
4 & 0 & 7 & 0 & 0 & 0 \\
3 & 4 ...
... 0 & 1 \\
1 & 0 & 0 & 3 & 4 & 0 \\
1 & 1 & 0 & 0 & 3 & 4
\end{array} \right] $](img71.gif)
![$\displaystyle A' = \left[ \begin{array}{rrrrrr}
4 & & 7 & & & \\
3 & 4 & & 2 &...
...
& & 7 & 4 & & 1 \\
1 & & & 3 & 4 & \\
1 & 1 & & & 3 & 4
\end{array} \right] $](img74.gif)