Il flusso dell'acqua in un mezzo poroso retto dall'equazione di Darcy:
dove:
Nel caso pigenerale il mezzo poroso da considerarsi non omogeneo e anisotropo. Il coefficiente di filtrazione diventa perciø un tensore funzione della posizione:
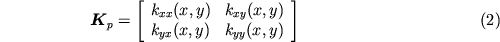
Se si assume la profondit dell'acquifero costante e pari a B
il moto risulta bidimensionale in un piano orizzontale.
In tal caso si puø definire un coefficiente di trasmissivit
caratteristico dell'acquifero: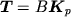 
.
Dal principio di conservazione della massa di acqua si ricava
l'equazione generale che regge il moto in un acquifero in pressione:
Ad essa vanno aggiunte le condizioni al contorno di Dirichlet o di Neumann:
Nella presente esercitazione si vuole
risolvere numericamente
il problema conservazione_massa
in un dominio circolare di centro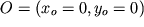 
e raggio unitario,
con trasmissivit costante ed unitaria.
Sull'intero dominio vi una ricarica uniforme e costante pari a f(x,y)=4.
Il problema da risolvere dunque il seguente:
con condizioni al contorno di Dirichlet:
La soluzione analitica di tale problema data da:
L'equazione esercitazione viene risolta utilizzando un metodo agli elementi finiti (FEM) con elementi triangolari e funzioni base lineari.
