



Next: Fattore incompleto di Cholesky
Up: gcm
Previous: Caso simmetrico
Indice
Una delle chiavi del successo del GCM nella soluzione efficiente di sistemi
lineari sparsi, simmetrici e definiti positivi sta nella possibilità di
ottenere formidabili accelerazioni della convergenza mediante l'uso di
opportune matrici di precondizionamento. La scelta di 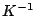 deve soddisfare
alle seguenti caratteristiche:
deve soddisfare
alle seguenti caratteristiche:
- deve essere tale che il prodotto
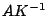 abbia lo spettro, cioè
l'insieme degli autovalori, raggruppato attorno all'unità e comunque un
numero di condizionamento spettrale inferiore a quello di
abbia lo spettro, cioè
l'insieme degli autovalori, raggruppato attorno all'unità e comunque un
numero di condizionamento spettrale inferiore a quello di 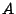 ;
;
- il calcolo deve essere semplice e poco costoso per non appesantire lo
schema;
- l'occupazione di memoria deve essere inferiore o al più paragonabile a
quella della matrice del sistema allo scopo di non vanificare lo sforzo
computazionale effettuato per la memorizzazione compatta.
Spesso le suddette caratteristiche confliggono fra loro e necessariamente la
scelta di 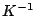 diventa il risultato di un compromesso. Per paradosso, la
matrice che soddisfa completamente la prima richiesta è ovviamente
diventa il risultato di un compromesso. Per paradosso, la
matrice che soddisfa completamente la prima richiesta è ovviamente 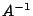 ,
il cui costo ed occupazione di memoria (si ricordi che l'inversa di una matrice
sparsa è generalmente una matrice piena) tuttavia rendono del tutto
incalcolabile.
,
il cui costo ed occupazione di memoria (si ricordi che l'inversa di una matrice
sparsa è generalmente una matrice piena) tuttavia rendono del tutto
incalcolabile.
Una discreta accelerazione del metodo del GC è ottenuta scegliendo:
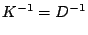 |
(20) |
dove 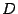 è la matrice diagonale contenente gli elementi diagonali
di
è la matrice diagonale contenente gli elementi diagonali
di 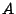 . In questo caso, il calcolo della matrice di precondizionamento e la
sua applicazione nello schema del GCM risultano banali e vengono lasciati per
esercizio al lettore. Il raggruppamento degli autovalori attorno all'unità
di
. In questo caso, il calcolo della matrice di precondizionamento e la
sua applicazione nello schema del GCM risultano banali e vengono lasciati per
esercizio al lettore. Il raggruppamento degli autovalori attorno all'unità
di 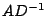 , tuttavia, può essere limitato, specialmente se
, tuttavia, può essere limitato, specialmente se 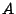 presenta
coefficienti extra-diagonali grandi rispetto agli elementi diagonali.
presenta
coefficienti extra-diagonali grandi rispetto agli elementi diagonali.
Risultati assai più significativi sono invece ottenuti assumendo:
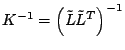 |
(21) |
dove 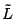 , matrice triangolare bassa, è calcolata mediante la
fattorizzazione incompleta di
, matrice triangolare bassa, è calcolata mediante la
fattorizzazione incompleta di 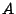 , cioè la decomposta di Cholesky a cui
viene assegnato il medesimo schema di sparsità di
, cioè la decomposta di Cholesky a cui
viene assegnato il medesimo schema di sparsità di 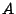 . L'uso di questa
matrice di precondizionamento, proposto negli anni '70 da Kershaw, si rivela
generalmente un ottimo compromesso fra le contrapposte esigenze precedentemente
discusse. Il calcolo di
. L'uso di questa
matrice di precondizionamento, proposto negli anni '70 da Kershaw, si rivela
generalmente un ottimo compromesso fra le contrapposte esigenze precedentemente
discusse. Il calcolo di 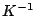 secondo la (21) e la sua applicazione
nell'algoritmo del GCM verranno esaminati nei due paragrafi seguenti.
secondo la (21) e la sua applicazione
nell'algoritmo del GCM verranno esaminati nei due paragrafi seguenti.
Subsections




Next: Fattore incompleto di Cholesky
Up: gcm
Previous: Caso simmetrico
Indice
Massimiliano Ferronato
2005-09-27
![]() deve soddisfare
alle seguenti caratteristiche:
deve soddisfare
alle seguenti caratteristiche:
![]() diventa il risultato di un compromesso. Per paradosso, la
matrice che soddisfa completamente la prima richiesta è ovviamente
diventa il risultato di un compromesso. Per paradosso, la
matrice che soddisfa completamente la prima richiesta è ovviamente ![]() ,
il cui costo ed occupazione di memoria (si ricordi che l'inversa di una matrice
sparsa è generalmente una matrice piena) tuttavia rendono del tutto
incalcolabile.
,
il cui costo ed occupazione di memoria (si ricordi che l'inversa di una matrice
sparsa è generalmente una matrice piena) tuttavia rendono del tutto
incalcolabile.