La matrice A è sparsa, reale, simmetrica e definita positiva ed è memorizzata in forma compatta.
Le matrici che consideriamo riguardano problemi di ingegneria strutturale e provengono dalla Harwell-Boeing Collection (una raccolta di matrici relative a varie applicazioni e sono disponibili in rete come matrici test per lo studio di algoritmi di algebra numerica).
Come precondizionatore si provi sia la decomposta incompleta di Cholesky che il precondizionatore diagonale.
Nel CGM si usi il vettore iniziale x0 ottenuto con 0, 1, 2,5, 10 e 20 iterazioni preliminari effettuate con lo schema delle Correzioni Residue.
I dettagli sui casi test e su cosa portare all'esame si trovano sulla dispensa.
Per ciascun caso test, si consideri come termine noto il vettore b dato dalla somma degli elementi di ciascuna riga di A in modo che la soluzione esatta sia data dal vettore x con elementi tutti uguali a 1.
Nei files di dati (del tipo matrice_prova.dat ) sono memorizzati, nell'ordine:
- N e NT , la dimensione del problema e il numero di elementi non nulli della matrice A
- il vettore SYSMAT
- il vettore JA
- il vettore IA
- Caso test 1
matrice nos4
la matrice è 100x100 con 347 elementi non nulli.

- Caso test 2
matrice_bcsstk01.dat
la matrice è 48x48 con 224 elementi non nulli.
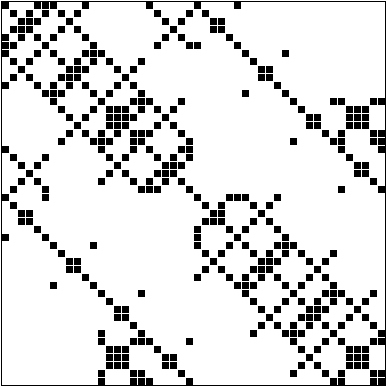
- Caso test 3
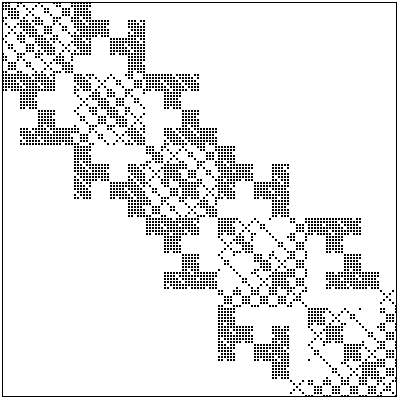
matrice bcsstk04
la matrice è di dimensione 132x132 ed ha 1890 elementi non nulli.
Ultimo aggiornamento: